Angle solide - Définition

Quelques exemples

Calotte sphérique dont le diamètre apparent est 2θ

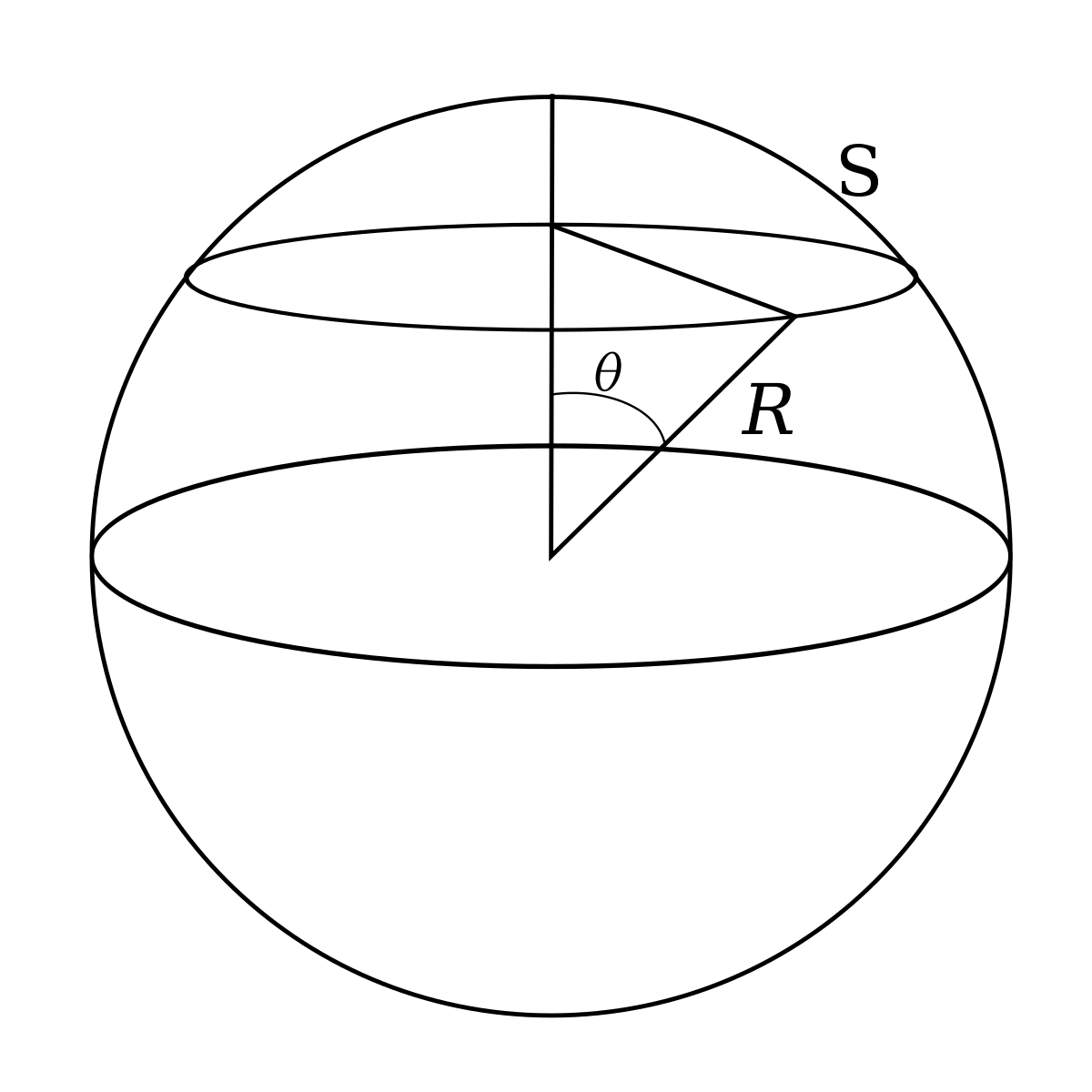
• En reprenant la définition de l'angle solide en coordonnées sphériques, les angles θ = π/3, θ = π/2 et θ = 2π/3 délimitent un découpage de la sphère en quatre surfaces égales de π stéradians. Ainsi, l'espace complet est vu sous un angle solide de 4π sr.
• Un hémisphère correspond donc à un angle solide de 2π sr.
• Un trièdre, formé par deux murs perpendiculaires et le sol (un octant, en mathématiques), découpe un angle solide de π/2 sr, soit un huitième de sphère.
• Entre la latitude de San Diego, en Californie, dans l'hémisphère nord et celle de Sydney, en Australie, dans l'hémisphère Sud, il y a la moitié de la surface terrestre, soit un angle solide de 2π sr.
• Entre le cercle polaire et le tropique du Cancer, dans l'hémisphère nord, il y a le quart de la surface terrestre, soit un angle solide de π sr.
• Les angles solides sous lesquels on voit une pièce d'un centime d'euro à 1,80 m de distance, la Lune et le Soleil, sont très proches : ≈6.10⁻⁵ sr (voir à ce sujet les éclipses solaires).
• Un « carré de ciel » de 0,923… radians de côté se voit sous un angle solide d'un stéradian. Évidemment, si le carré est "très petit", on le mesure banalement en mas^2 ( milliarcseconde*milliarcseconde ).