Angle solide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
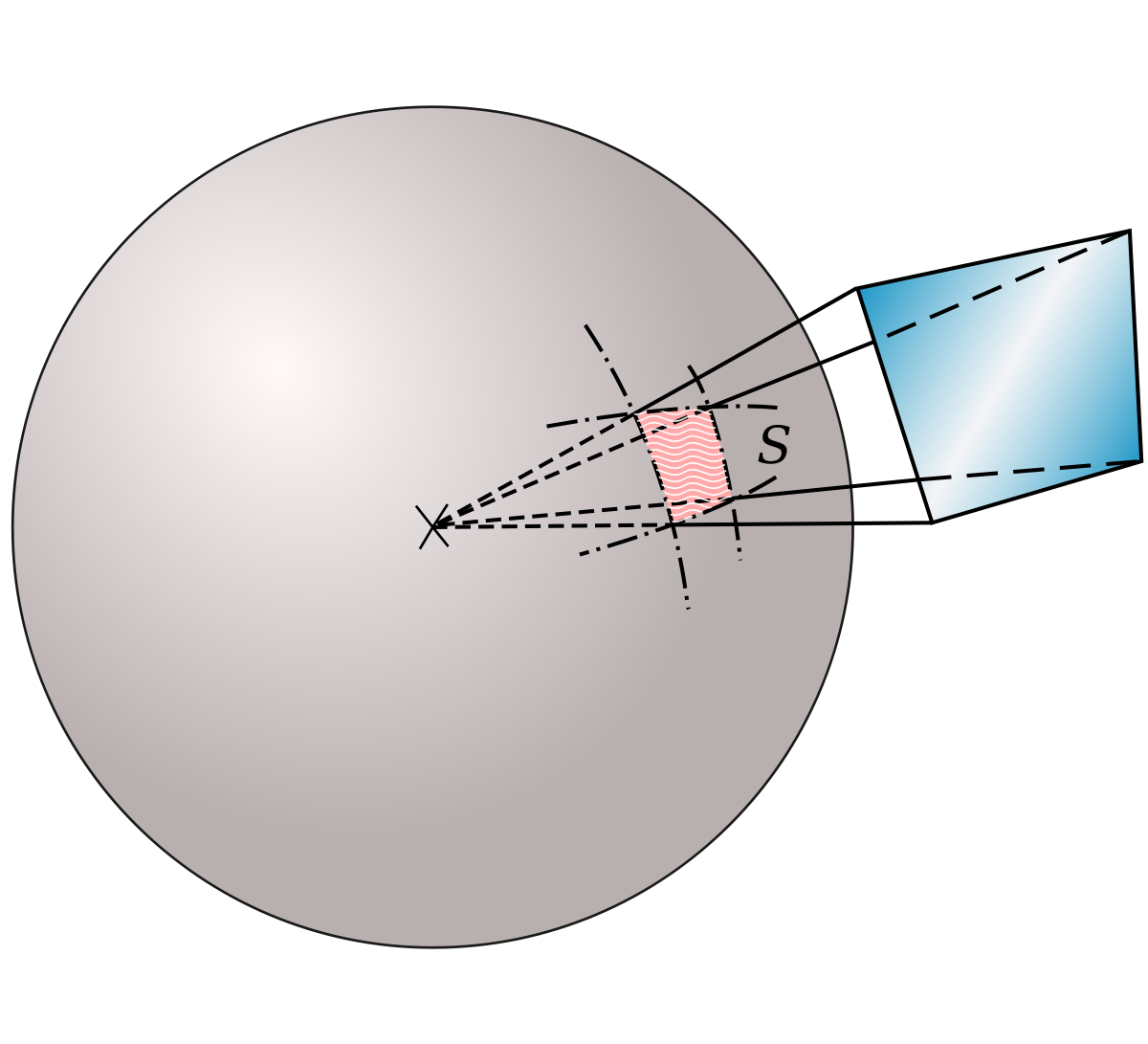
En mathématiques, en géométrie et en physique, un angle solide est l'analogue tridimensionnel de l'angle plan ou bidimensionnel.
L'angle plan étant défini, dans l'espace bidimensionnel, comme le rapport de la longueur de l'arc sur le rayon d'un cercle, l'angle solide, dans l'espace tridimensionnel, est défini de façon analogue comme le rapport de la surface d'une partie d'une sphère sur le rayon au carré. Son unité est le stéradian noté sr.
On le note souvent Ω (oméga majuscule). Il mesure la surface sur laquelle un objet se projette radialement sur une sphère de rayon unité.
Calcul
Formule usuelle
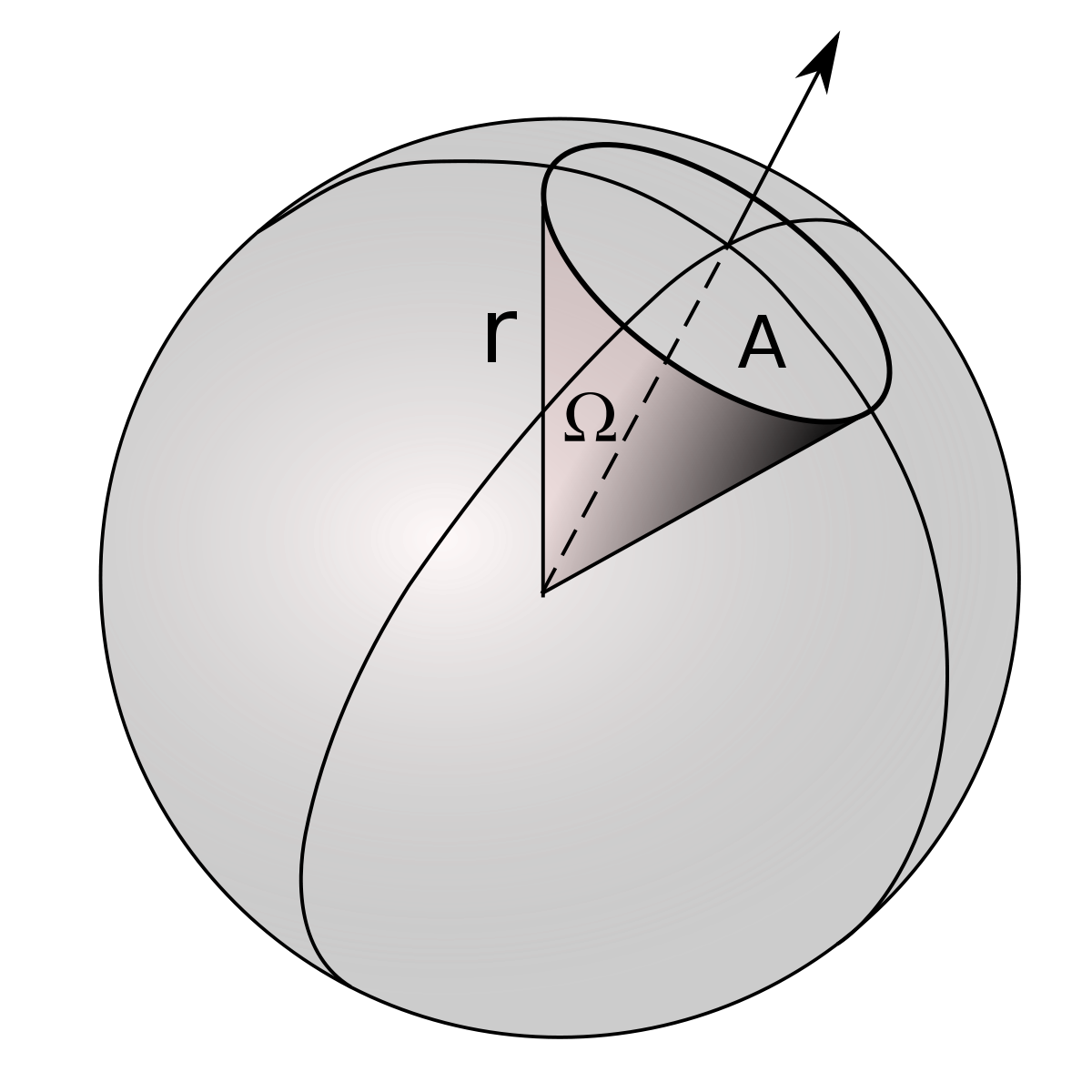
Pour calculer l'angle solide sous lequel on voit un objet à partir d'un point donné, on projette l'objet sur une sphère de rayon R centrée en ce point.
Si la surface que cette projection fait sur la sphère est S, l'angle solide sous lequel l'observateur voit l'objet est, par définition :
Avec :
- Ω : en Stéradian (sr)
- S : en Mètre carré (m2)
- R : en Mètre (m)
La notion d'angle solide intervient en particulier dans la définition de la luminosité et de ses grandeurs dérivées. En général, ces grandeurs sont associées à des corps sources ou récepteurs dont les positions spatiales sont exprimées en coordonnées curvilignes (par exemple, en coordonnées sphériques : position des étoiles, satellites, capteurs au sol, etc.). On peut dès lors définir l'angle solide dans ce type de coordonnées.
Angle solide en coordonnées sphériques
Pour une sphère de rayon r, l'angle solide est défini pour un élément de surface élémentaire d2 S, c'est-à-dire engendré par des variations angulaires infinitésimales des zénith θ et azimut φ (la surface élémentaire est assimilée à un plan) :
D'où :
Par intégration dans les domaines angulaires des coordonnées sphériques :
Ceci définit un cône de révolution de demi-angle au sommet α et de base "sphérique"
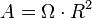
![h = R \cdot [cos\ \alpha - cos\ \alpha']](https://static.techno-science.net/illustration/Definitions/autres/f/f8207fc5d89c285d5ff2ab59c24678c9_c2ddf11779c7a0661ce0f4ec66cc2f32.png)
Coin d'un tétraèdre
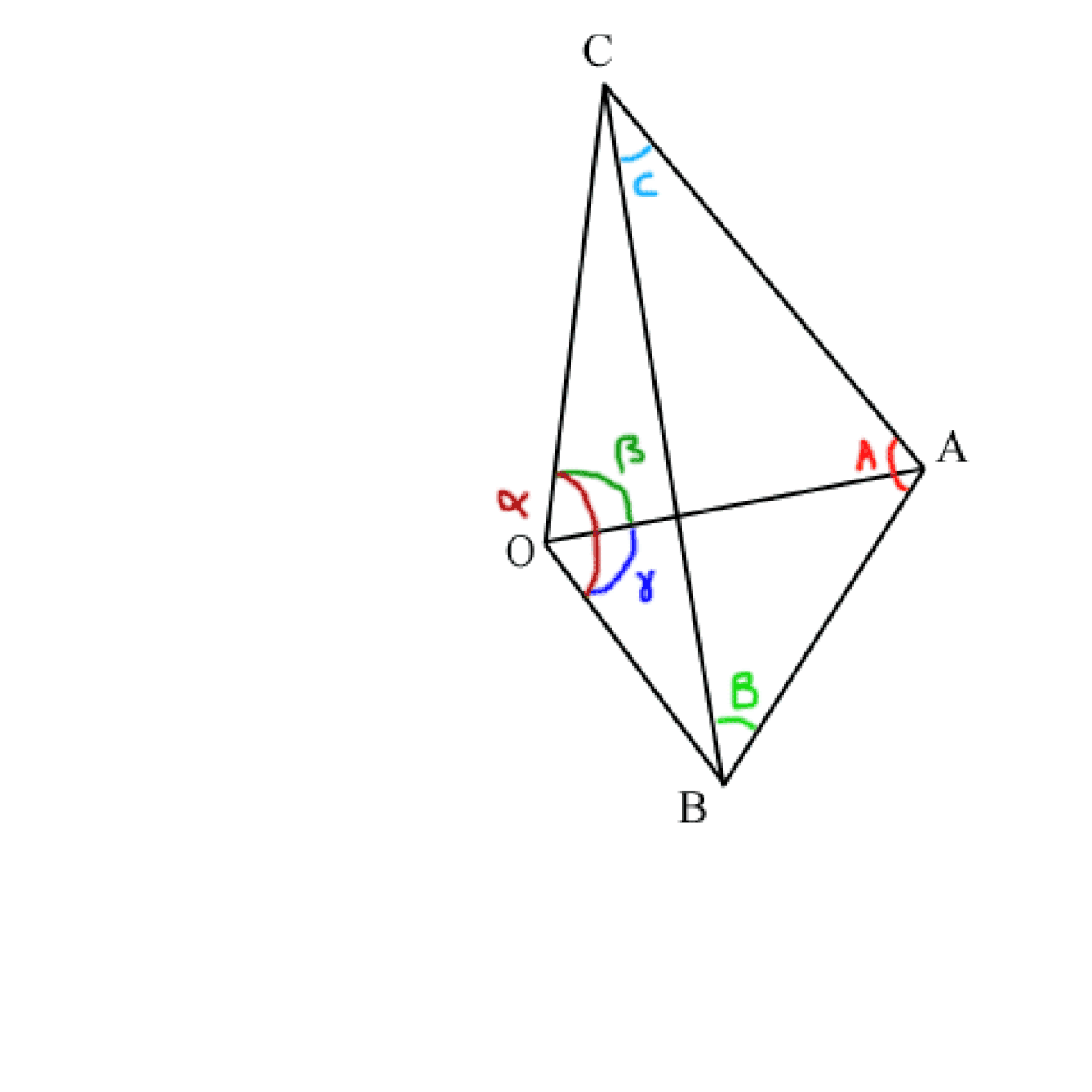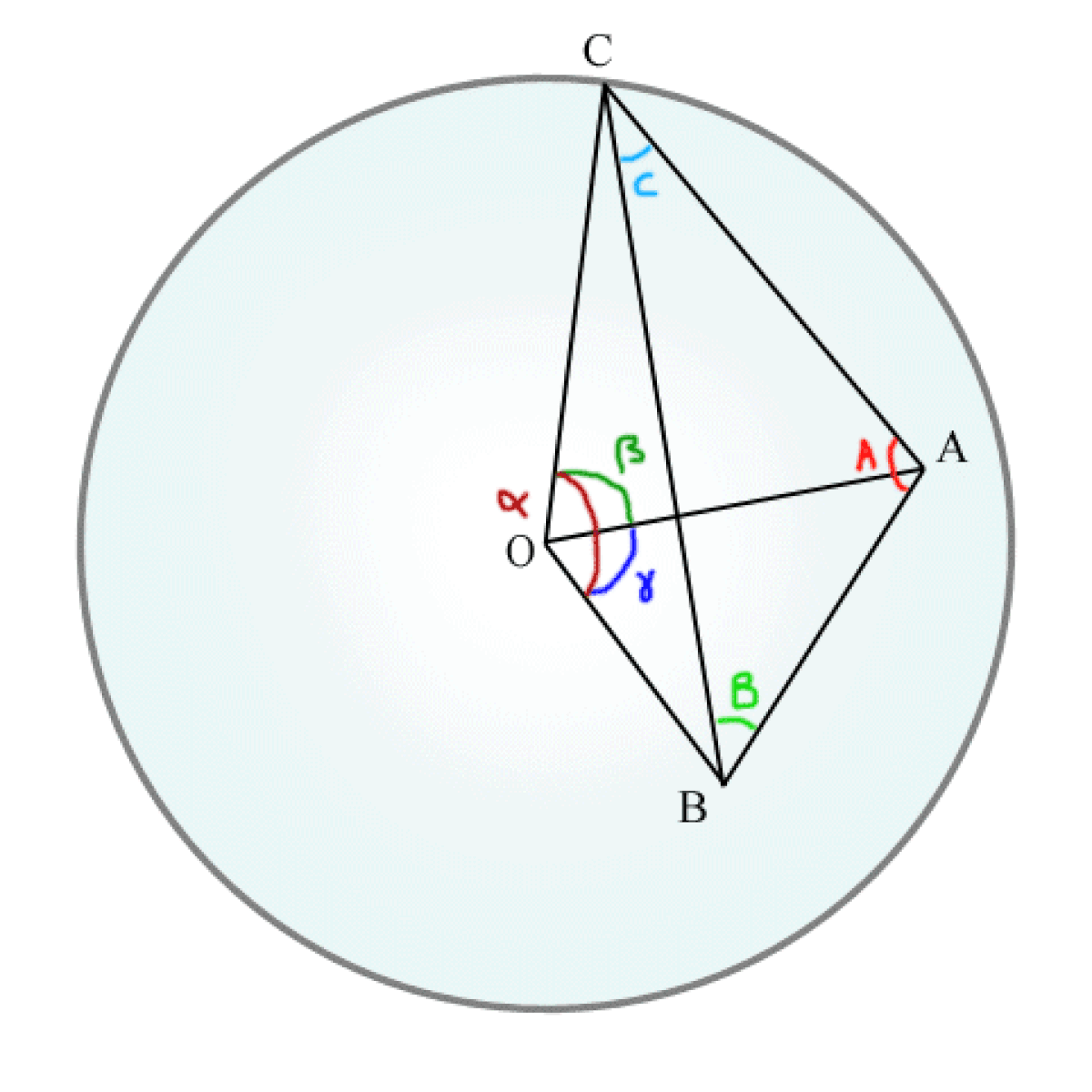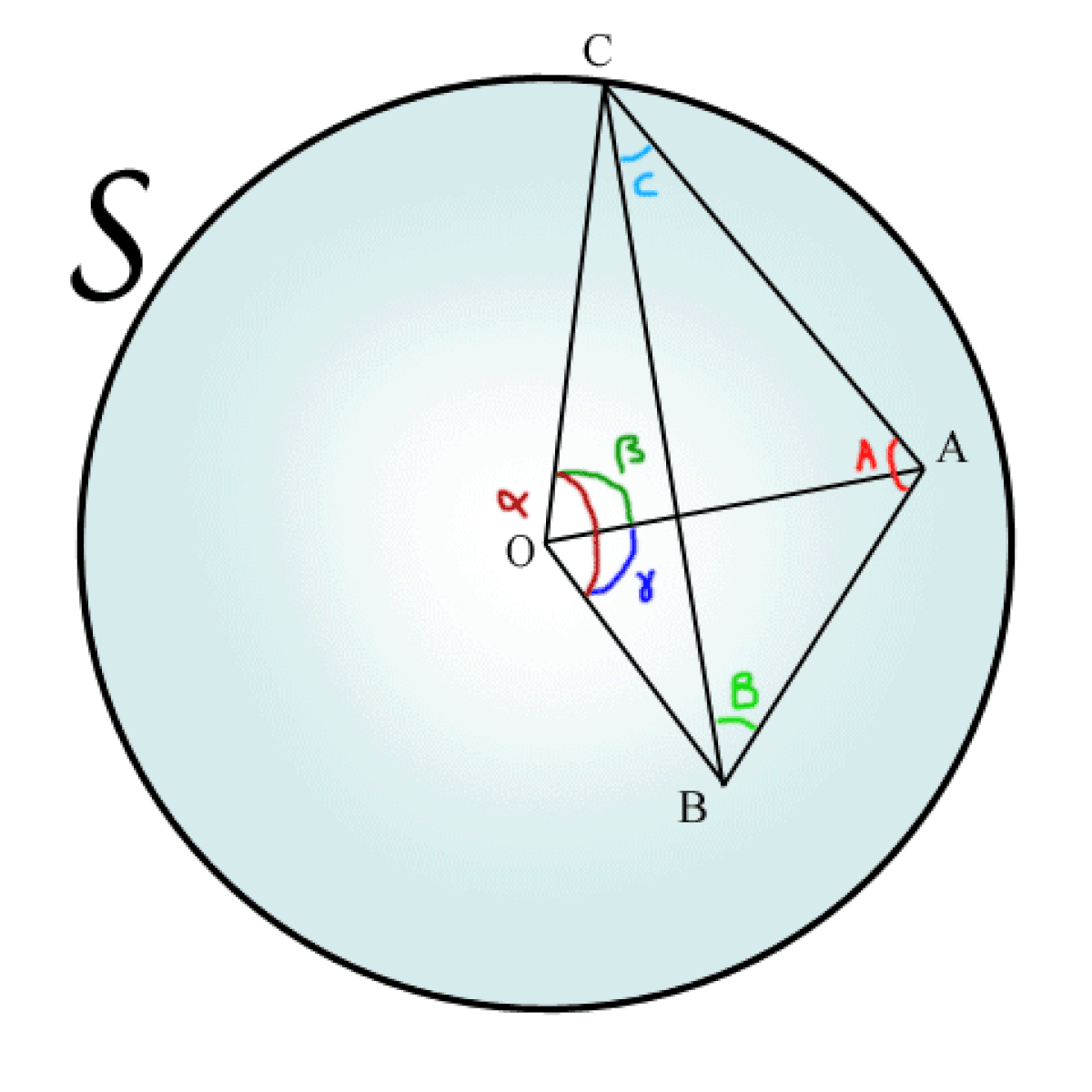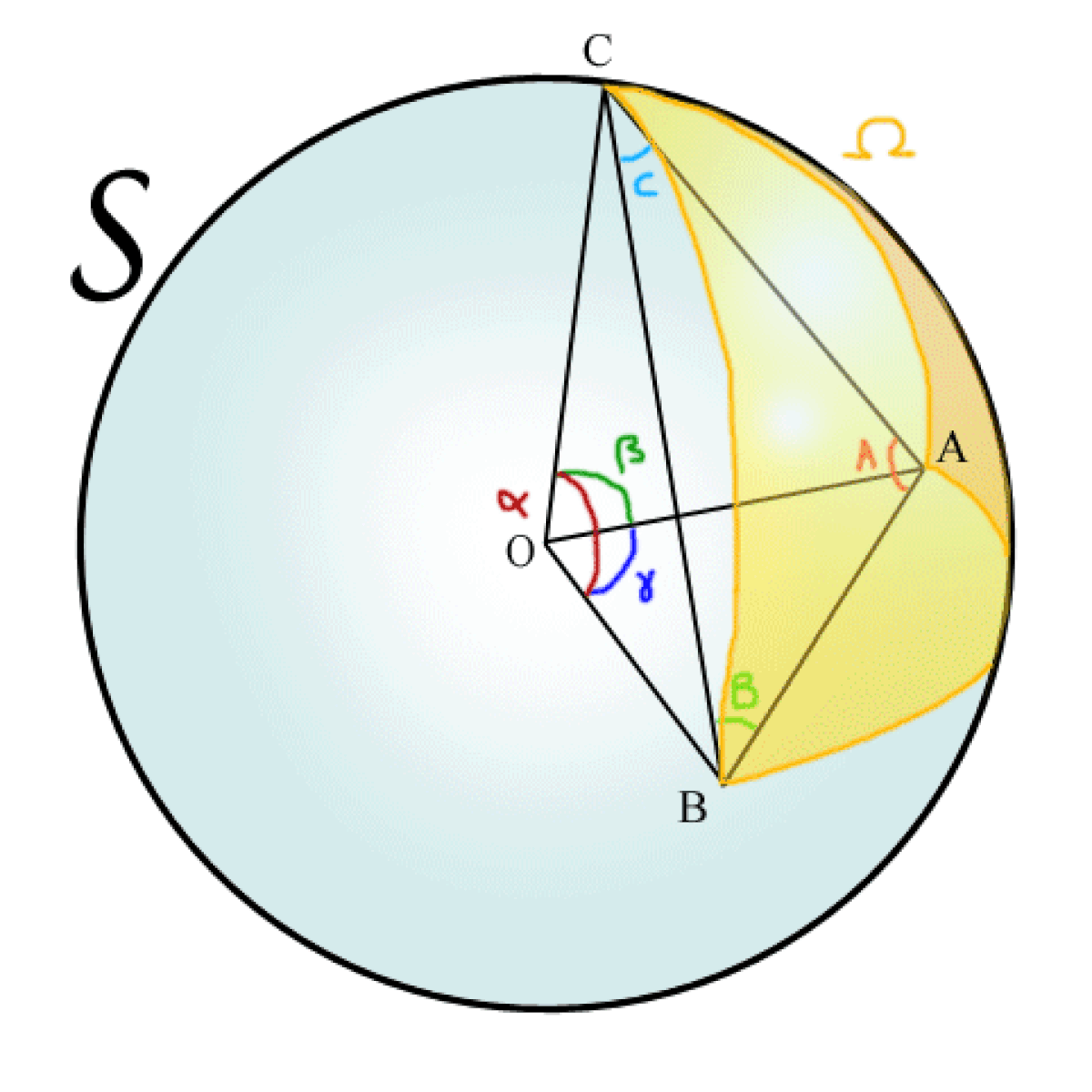
Soit Ω l'angle solide formé par un triangle sphèrique. Le théorème de l'excès sphérique dit de Gauss-Bonnet indique :
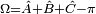
- démonstration. : c'est un jeu de décomptage-coloriage : colorer le dièdre complet A en jaune (angle solide (2A)*2), le dièdre B en cyan (les deux côtés AC et BC vont apparaître verts ainsi que le triangle sphérique. Recommencer par le dièdre A en jaune et le dièdre C en magenta , le triangle apparaîtra en rouge-vermillon. Recommencer enfin par le dièdre B en cyan et le dièdre C en magenta , le triangle apparaîtra en bleu-violet. La figure se voit très bien dans l'article de trigonométrie sphérique. Si on fait les trois à la fois, on aura recouvert la sphère entière 2 fois (surface 2* 4π) SAUF le triangle sphérique ABC, NOIR qui a été recouvert 6 fois, soit un AJOUT de (6-2) fois Ω (ainsi que son symetrique à l'antipode, soit encore 2Ω); donc :
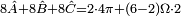
- Ce résultat, découvert par Thomas Harriot, mais non publié, fut édité par Albert Girard vers 1625.Gauss puis Bonnet généraliserons, bien plus tard.
- Quelques explications sur le site du Palais de la découverte
Les angles du triangle sphérique A, B et C suivent le théorème de Pythagore-AlKashi modifié, énoncé en trigonométrie sphérique par Al-Battani Viète et Gauss :
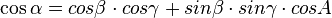
- [démonstration : effectuer le produit scalaire
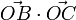
ce qui peut se réécrire :
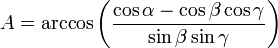
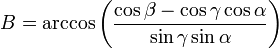
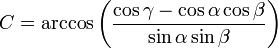
avec
Cas particuliers :
-
- Si jamais l'un des trois angles du tétraèdre α, β ou γ devient nul, alors les deux autres se superposent et deviennent égaux : l'angle solide Ω s'aplatit et devient alors nul.
- Si
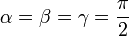
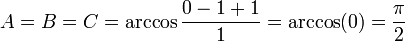
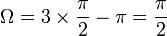
- Si α + β + γ = 2π (tétraèdre plat), alors A = B = C = arccos( − 1) = π (angle sphérique plat : équateur) et Ω = 2π (demi sphère).
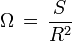
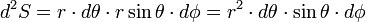
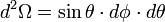
![\Omega = \iint d^2\Omega = \int_0^{2\pi} d\phi \int_0^{\alpha} \sin\theta \ d\theta \ = 2\pi\int_0^{\alpha} \sin \theta \ d \theta = 2\pi\left[ -\cos \theta \right]_0^{\alpha} \ = 2\pi\left(1 -\cos \alpha \right)](https://static.techno-science.net/illustration/Definitions/autres/c/c29f0db778d162073d42baf3c5f75a52_2d0746104d9a82836fc4afa5a1f92e0e.png)

















































