Compacité (mathématiques) - Définition

Introduction

En topologie, on dit d'un espace séparé qu'il est compact, ou qu'il vérifie la propriété de Borel-Lebesgue, si chaque fois qu'il est recouvert par des ouverts, il est recouvert par un nombre fini d'entre eux. Le nom choisi pour cette propriété rend hommage aux mathématiciens français Émile Borel et Henri Lebesgue, car le théorème qui porte leur nom établit que tout segment de la droite réelle est compact, et plus généralement, que les compacts de sont les fermés bornés. Une approche plus intuitive de la compacité dans le cas particulier des espaces métriques est détaillée dans l'article Compacité séquentielle.

Propriété de Borel-Lebesgue

Définition préalable : Soit E un ensemble, et A une partie de E. On dit qu'une famille de parties de E recouvre A si leur réunion contient A.

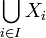
Propriété de Borel-Lebesgue pour les segments : soit un segment [a,b] de la droite réelle. De tout recouvrement de ce segment par des ouverts, on peut extraire un sous-recouvrement fini. C'est-à-dire que pour toute famille d'ensembles ouverts recouvrant [a,b], il existe une partie finie J de I telle que la sous-famille recouvre [a,b].

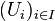
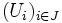
Pour une démonstration de cette propriété voir le théorème de Borel-Lebesgue, aussi appelé théorème de Heine-Borel.

La propriété de Borel-Lebesgue est étroitement liée à une propriété des suites bornées de réels : de toute suite bornée de réels, on peut extraire une suite convergente. Le lien entre les deux propriétés est explicité plus bas (dans la section ).

De l'une ou l'autre de ces propriétés il est possible de tirer quelques conséquences importantes sur les fonctions numériques. Notamment : l'image d'un segment par une application continue est non seulement (d'après le théorème des valeurs intermédiaires) un intervalle, mais c'est même un segment (théorème des bornes), et la fonction est alors uniformément continue (théorème de Heine).

La propriété de Borel-Lebesgue (de même que la compacité séquentielle) peut se formuler comme une propriété intrinsèque de l'espace topologique étudié (ici : l'espace [a,b] muni de sa topologie usuelle), indépendamment du fait que celui-ci soit, éventuellement, inclus dans un espace topologique "plus gros" (ici : ), et soit muni de ce fait de la topologie induite. En ce sens, la notion de "partie compacte" (d'un espace topologique) diffère fondamentalement de celle, par exemple, de "partie fermée".

Définition par la théorie des filtres

Un espace topologique séparé est compact si et seulement si pour tout filtre F sur E, il existe un filtre plus fin que F qui converge, ou encore si et seulement si tout ultrafiltre sur E converge. Cette définition équivalente est rarement utilisée. Elle est particulièrement adéquate pour prouver que tout produit de compacts est compact.

Axiome de Borel-Lebesgue et définition générale des compacts

Un espace topologique E est dit quasi-compact s'il vérifie l'axiome de Borel-Lebesgue : de tout recouvrement ouvert de E, on peut extraire un sous-recouvrement fini. L'espace est dit compact quand il est en outre séparé au sens de Hausdorff (T2).

Par passage au complémentaire, cette dernière propriété est équivalente à la propriété suivante : si est une famille de fermés telle que , alors on peut extraire une famille finie , avec , telle que . Ou encore, par contraposition, si toute intersection finie d'une famille de fermés est non vide, alors l'intersection de toute la famille est non vide.

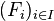
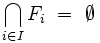
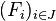
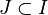
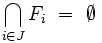
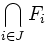
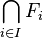
NB : En terminologie anglo-saxonne, la définition est légèrement différente. Sauf mention contraire, le compact anglophone est un quasi-compact francophone, et la notion de quasi-compacité n'existe pas. Toutes les propriétés ne s'appliquent donc pas en général, sauf sous l'hypothèse que l'espace est séparé.