Compacité (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Exemples
- Tout espace fini séparé est compact. Chaque point est en effet recouvert par un ouvert, le sous-recouvrement comportant un ouvert par point est fini, ce qui montre la compacité.
- L'ensemble constitué des images d'une suite convergente ainsi que de la limite dans un espace séparé est compact. En effet, de tout recouvrement ouvert, on peut extraire un ouvert contenant la limite, comme il n'existe qu'un nombre de points fini hors de cet ouvert, il est aisé de trouver un sous-recouvrement fini.
Propriétés
Compacts et fermés
Dans un espace séparé, deux parties compactes disjointes sont toujours incluses dans deux ouverts disjoints.
Soient A et B deux parties disjointes d'un espace séparé E qui, munies de la topologie induite, sont compactes. Montrons qu'il existe deux ouverts disjoints U, V de E, dont l'un contient A et l'autre B.
- On le démontre d'abord dans le cas particulier où B est réduit à un point b (n'appartenant pas à A). Comme E est séparé, pour tout point a de A, il existe deux ouverts disjoints Oa, Wa de E, dont le premier contient a et le second, b. La famille
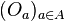
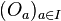
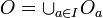
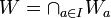
- On en déduit le cas général (B compact quelconque) par une méthode analogue : pour chaque point b de B il existe (d'après le cas particulier) deux ouverts disjoints Ub, Vb de E dont le premier contient A et le second, b (ce sont le O et le W construits précédemment, mais indexés à présent par b qui varie dans B). La famille
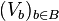
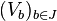
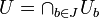
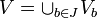
Toute partie compacte d'un espace séparé est fermée.
- Preuve : soit A une partie compacte d'un espace séparé E. Montrons que son complémentaire B est ouvert. Pour tout point b de B, d'après la propriété précédente, il existe un ouvert W contenant b et disjoint d'un ouvert contenant A. Un tel W est a fortiori disjoint de A donc inclus dans B. Par conséquent B est voisinage de tous ses points, donc ouvert.
- NB : Ceci est en général faux si l'espace ambiant n'est pas séparé ; par exemple dans

Toute partie fermée d'un espace compact est compacte.
Preuve : Soient C un espace compact et F une partie fermée de C. Remarquons d'abord que F (muni de la topologie induite) est encore séparé. Montrons ensuite qu'il vérifie la propriété de Borel-Lebesgue. Soit (Fi ) une famille de fermés de F dont toute intersection finie est non vide. Comme les Fi sont aussi des fermés du compact C, leur intersection est non vide, ce qui conclut.
Un espace compact est normal.
Preuve : dans un espace compact E, soient A, B deux fermés disjoints. D'après les propriétés ci-dessus, A et B sont alors deux compacts disjoints et E est séparé, si bien que A et B sont inclus dans deux ouverts disjoints, ce qui prouve que E est normal.
Autres propriétés
Les compacts de l'ensemble des nombres réels, muni de sa topologie usuelle, sont les fermés bornés.
Ce résultat est connu sous le nom de théorème de Borel-Lebesgue.
Le produit cartésien de compacts, munis de la topologie produit est compact.
Ce résultat est connu sous le nom de théorème de Tychonov.
Dans un espace vectoriel normé de dimension finie sur le corps des réels ou des complexes, les compacts sont les fermés bornés.
En effet, par équivalence des normes, cet énoncé se ramène à la caractérisation des compacts de

Compacité et continuité
L'image d'un compact, par une application continue à valeurs dans un espace séparé, est compacte.
Considérons un recouvrement ouvert de f(C), son image réciproque par f est un recouvrement ouvert de C. On peut en extraire un sous-recouvrement fini, l'image par f de ce sous-recouvrement est un sous-recouvrement de C extrait du recouvrement initial. L'existence d'un tel sous-recouvrement démontre la compacité de f(C).
Un premier exemple d'usage de ce résultat est le théorème des bornes, stipulant que l'image d'un segment par une application continue de R dans R atteint ses bornes (ici R désigne l'espace des réels).
Un deuxième exemple est la démonstration du caractère isopérimétrique d'un polygone régulier, question ouverte depuis l'antiquité. L'objet est de savoir quel est le polygone à n côtés qui possède la plus grande aire, pour un périmètre donné. Des raisonnements géométriques assez simples montrent que l'unique candidat possible est le polygone régulier, résultat démontré depuis l'antiquité grecque. En revanche, l'existence d'une solution à cette question est restée ouverte jusqu'au XIXe siècle.
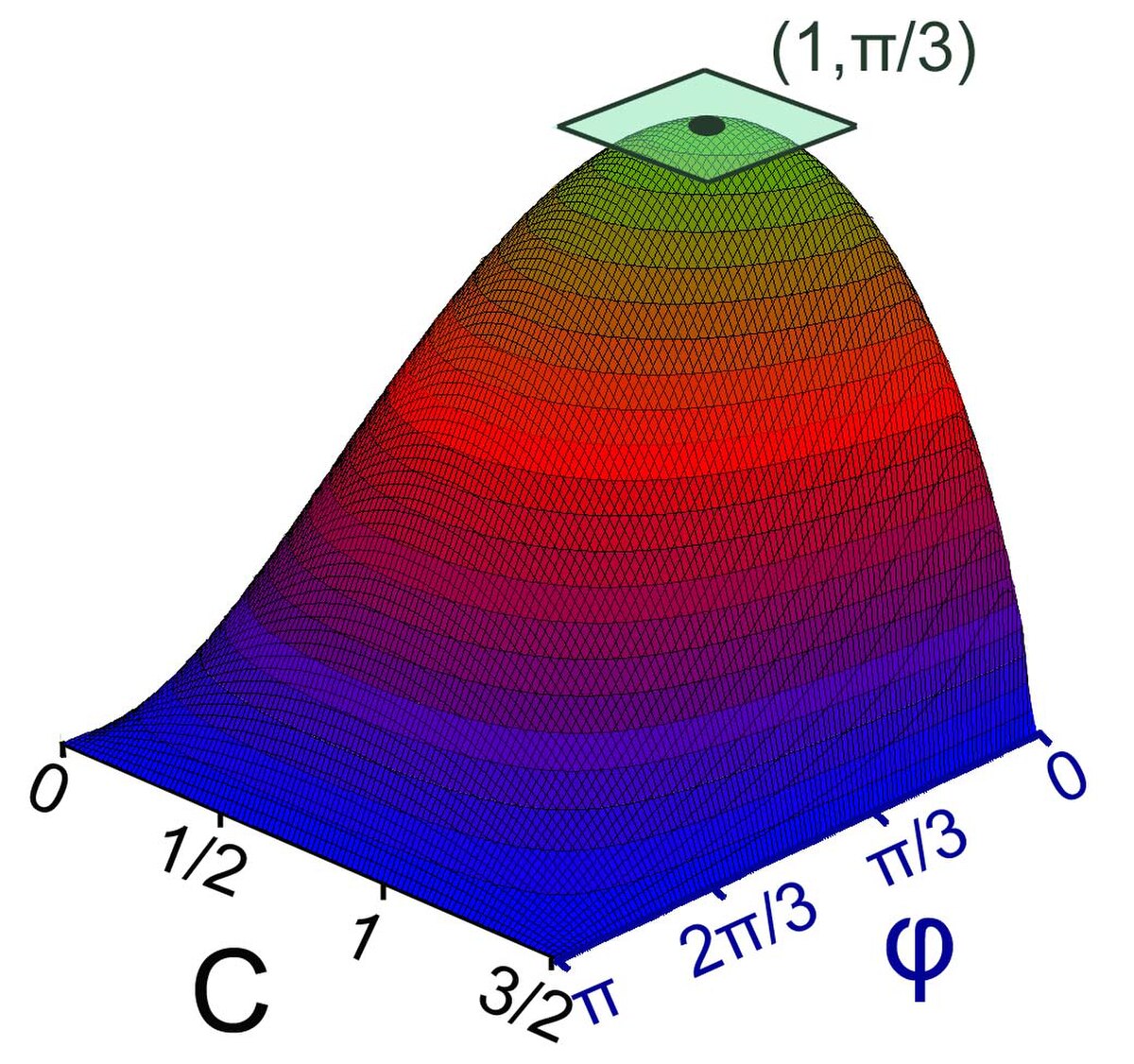
Pour comprendre la nature de la démonstration, le plus simple est de considérer le cas du triangle, illustré sur la figure de droite. Les triangles considérés sont tous de périmètre 3, ils sont identifiés à un couple (c, φ) où c désigne la longueur d'un côté et φ l'angle entre deux côtés dont l'un est celui de longueur c. La fonction f est celle qui, à un couple, associe la surface du triangle. Il n'est nécessaire que d'étudier la zone où c est compris entre 0 et 3/2 et φ entre 0 et π. Cette zone est un compact de R2. L'application f est continue, elle atteint donc son maximum, en l'occurrence au point (1, π/3). L'existence de ce maximum était le chaînon manquant pour une démonstration complète.
Pour le triangle, un peu d'analyse permet tout aussi bien de démontrer le résultat. Pour le cas général du polygone à n côtés, il n'est pas bien difficile de construire une démonstration analogue à celle présentée ici, grâce à la notion de compact. La solution analytique est en revanche vraiment lourde. Une démonstration détaillée est présentée dans l'article théorème isopérimétrique.
Un corollaire du théorème sur l'image continue d'un compact est :
Toute application continue d'un espace compact dans un espace séparé est fermée. En particulier, si elle est bijective alors c'est un homéomorphisme.
Théorème de Bolzano-Weierstrass et compacité séquentielle
Lorsque K est un espace métrique (automatiquement séparé), le théorème de Bolzano-Weierstrass énonce que K est compact si et seulement si de toute suite d'éléments de K il est possible d'extraire une sous-suite qui converge vers un élément de K, ou, de manière équivalente, toute suite admet une valeur d'adhérence.
Pour cette raison, dans le cadre des espaces métriques, la propriété de compacité est fréquemment introduite par caractérisation séquentielle.