Connexion de Koszul - Définition
La liste des auteurs de cet article est disponible ici.
Applications
Transport parallèle
Si c est une courbe différentiable de B, une section s de E le long de c est dite parallèle lorsqu'elle vérifie l'équation différentielle :
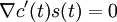
Calcul différentiel extérieur
Une fois fixé une connexion

![d^{\nabla}\left[\alpha\otimes s\right]=d\alpha\otimes s+ \alpha\wedge \nabla s](https://static.techno-science.net/illustration/Definitions/autres/f/facc0ce8f0cdb60e6f28770cf2fa1fb3_ffe680294cdc8bb474b2e5a2d64d56fa.png)
où
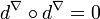
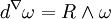
Identité de Bianchi :
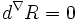
Construction de connexions
Transport de connexions
A toute application différentiable
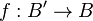

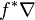
![\left[f^*\nabla\right]_X\left[s\circ f\right]=\left[\nabla_Xs\right]\circ f](https://static.techno-science.net/illustration/Definitions/autres/c/c888623b03f36d43dd9cacdd4fdc1faf_aaacf1bfe286528a97d2c90728cc45ac.png)
En particulier, si c:
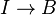

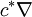
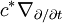
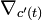
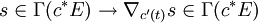
Cet opérateur vérifie la règle de leibniz:
![\left[\nabla_{c'(t)}\left[fs\right]\right](t)=f'(t)s(t)+f(t)\left[\nabla_{c'(t)}s\right](t)](https://static.techno-science.net/illustration/Definitions/autres/5/57d2b6ed3cad588fd4b02497f83d49d4_795e6e0cf877f9737d125fc867cc47c9.png)
Somme et produit tensoriel
Soient
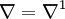
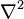
- Une connexion sur la somme directe
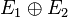
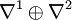
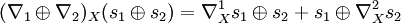
- Une connexion sur le produit tensoriel
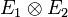
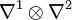
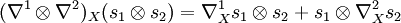
- Une connexion sur le fibré dual E* :
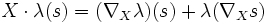
- Une connexion sur le fibré End(E1,E2) :
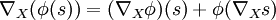
Connexion de Levi-Civita
Une métrique riemannienne g sur une variété différentielle M est un champ de formes bilinéaires symétriques définies positives. Plus exactement, une métrique g de classe Ck est la donnée en tout point x d'un produit scalaire gx sur l'espace tangent TxM, de sorte que pour tous champs de vecteurs X et Y sur M de classe Ck, la fonction g(X,Y) soit différentiable de classe Ck.
Si
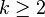
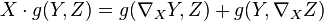
La courbure d'une variété riemannienne réfère à la courbure de sa connexion de Levi-Civita. La connexion de Levi-Civita est importante car elle capte une forte information sur la géométrie locale et globale. On distingue habituellement les variétés de courbure nulle, de courbure positive et de courbure négative. Les variétés riemanniennes "à courbure constante" servent de modèle de comparaison.

















































