Variété différentielle - Définition

Introduction

En mathématiques, les variétés différentielles ou variétés différentiables sont les objets de base de la topologie différentielle et de la géométrie différentielle. Il s'agit de variétés sur lesquelles il est possible d'effectuer les opérations du calcul différentiel et intégral.

Une variété différentielle se définit d'abord par la donnée d'une variété topologique, espace topologique localement homéomorphe à l'espace euclidien . Les homéomorphismes locaux sont appelés cartes et définissent des systèmes de coordonnées locales. La structure différentielle est définie en exigeant certaines propriétés de régularité des applications de transition entre les cartes. Cette structure permet par exemple de donner une définition globale de la notion d'application différentiable.

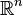
Définition par un atlas

Pour une introduction informelle voir l'article Variété (géométrie).

Cartes locales et atlas

L'application de projection stéréographique définit une carte locale sur la sphère.

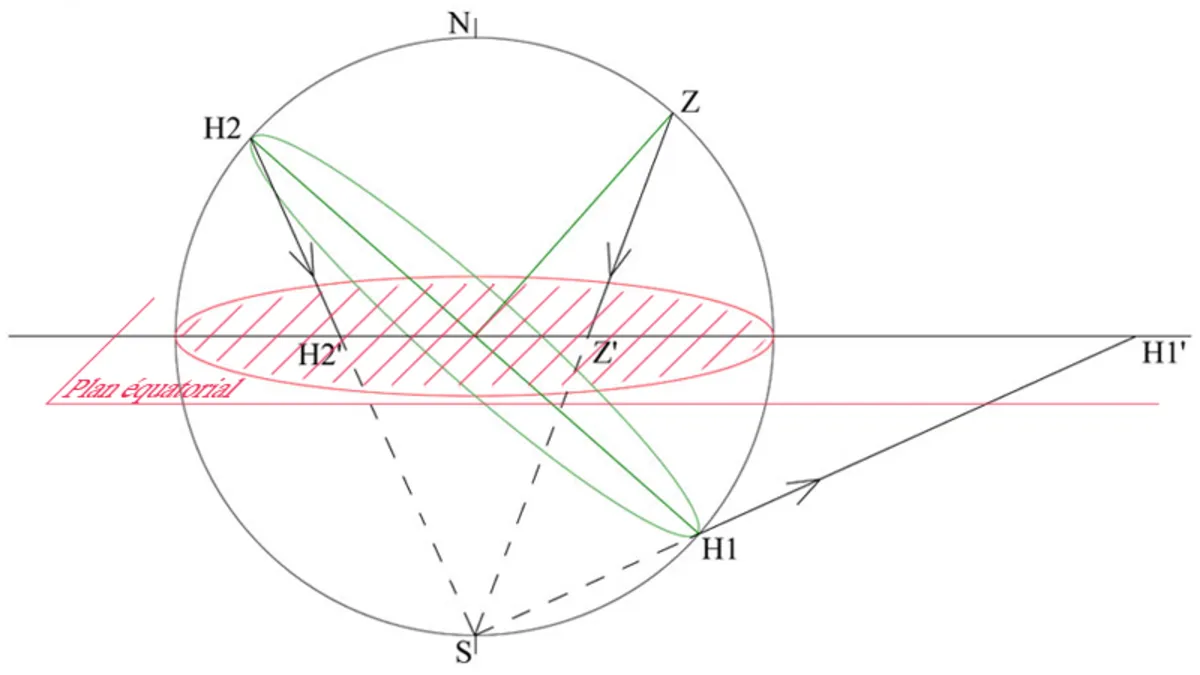
Une variété topologique M de dimension n est un espace topologique séparé à base dénombrable, tel que chacun de ses points admet un voisinage ouvert homéomorphe à un ouvert de l'espace vectoriel topologique . Plus précisément :

, il existe un voisinage ouvert U_x et un homéomorphisme . On dit alors que est une carte locale de M.

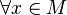
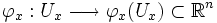
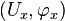
Une famille de cartes qui recouvre (entièrement) M constitue un atlas de la variété M.

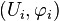
Un tel atlas est dit de classe C^k, si : pour tous les indices i,j tels que , l'application de changement de cartes

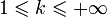
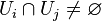
est un difféomorphisme de classe C^k.

Structure de variété différentielle

Deux atlas de classe C^k sur une même variété topologique M sont dits compatibles lorsque leur réunion est encore un atlas de classe C^k. La relation de compatibilité ainsi introduite est une relation d'équivalence pour les atlas.

Les classes d'équivalence définissent la structure de variété différentielle : une variété différentielle (ou variété différentiable) de classe C^k est une variété topologique munie d'une famille d'atlas de classe C^k tous compatibles avec un atlas donné.

Dans chaque classe d'équivalence existe un représentant privilégié, l'atlas maximal, obtenu en considérant toutes les cartes compatibles avec l'atlas initial.

Les exemples les plus classiques de variétés différentielles sont les ouverts de l'espace euclidien , la sphère de dimension n, le tore de dimension n, les espaces projectifs réels ou complexes.

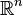
Variantes

On obtient une variété analytique en exigeant que les applications de changements de cartes soient des fonctions analytiques.

La géométrie complexe étudie les variétés analytiques complexes (ou variétés complexes), définies de façon analogue sur le corps des complexes, avec des applications de changement de cartes qui sont biholomorphes.

Il est possible d'étudier des variétés modelées sur des espaces vectoriels de dimension infinie, comme les variétés de Banach ou de Fréchet.

Calcul différentiel sur une variété

Vecteurs tangents et différentielle d'une application

On peut définir de façon relativement simple la notion de vecteur tangent à une sous-variété de , et cette définition donne des vecteurs de l'espace ambiant. Cependant, il est utile et important de disposer d'une construction qui ne fasse pas intervenir de plongement, mais qui soit valable au niveau des variétés abstraites.

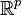
Un mode de définition possible est basé sur la relation de tangence entre les courbes. On peut, par lecture dans une carte locale, définir la notion de courbes tangentes en un point m de la variété M. Les vecteurs tangents en m à la variété sont alors les classes d'équivalence pour cette relation. Ils forment un espace vectoriel T_mM qui a la même dimension n que M.

La réunion disjointe de tous les espaces tangents T_mM pour m appartenant à M forme une variété TM de dimension 2n, appelée fibré tangent à la variété. L'espace TM possède une structure de fibré vectoriel de base M. Cependant cette construction engendre une perte de différentiabilité : si M est de classe C^k+1, le fibré tangent est de classe C^k.

On peut ensuite définir la différentielle d'une application différentiable f entre deux variétés M et N. On note m un point de M et n son image ; alors la différentielle T_mf de f au point m est une application linéaire de l'espace tangent T_mM vers T_nN. Pour la définir, on réintroduit les applications f_φ,ψ représentant la fonction f lue dans des cartes locales, et on en prend la différentielle au point φ ^{− 1}(m) correspondant à m. Une nouvelle fois, l'objet ainsi construit est indépendant des cartes utilisées.

Fibrés associés

Opérateurs de calcul différentiel