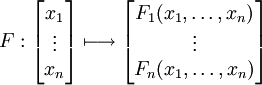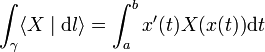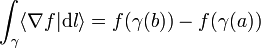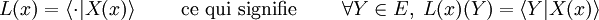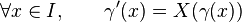Champ de vecteurs - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
| Articles d'analyse vectorielle | |

| |
| Objets d'étude | |
| Champ vectoriel | Champ scalaire |
| Équation aux dérivées partielles | |
| de Laplace | de Poisson |
| Opérateurs | |
| Nabla | Gradient |
| Rotationnel | Divergence |
| Laplacien scalaire | Bilaplacien |
| Laplacien vectoriel | D'alembertien |
| Théorèmes | |
| de Green | de Stokes |
| de Helmholtz | de flux-divergence |
| du gradient | du rotationnel |

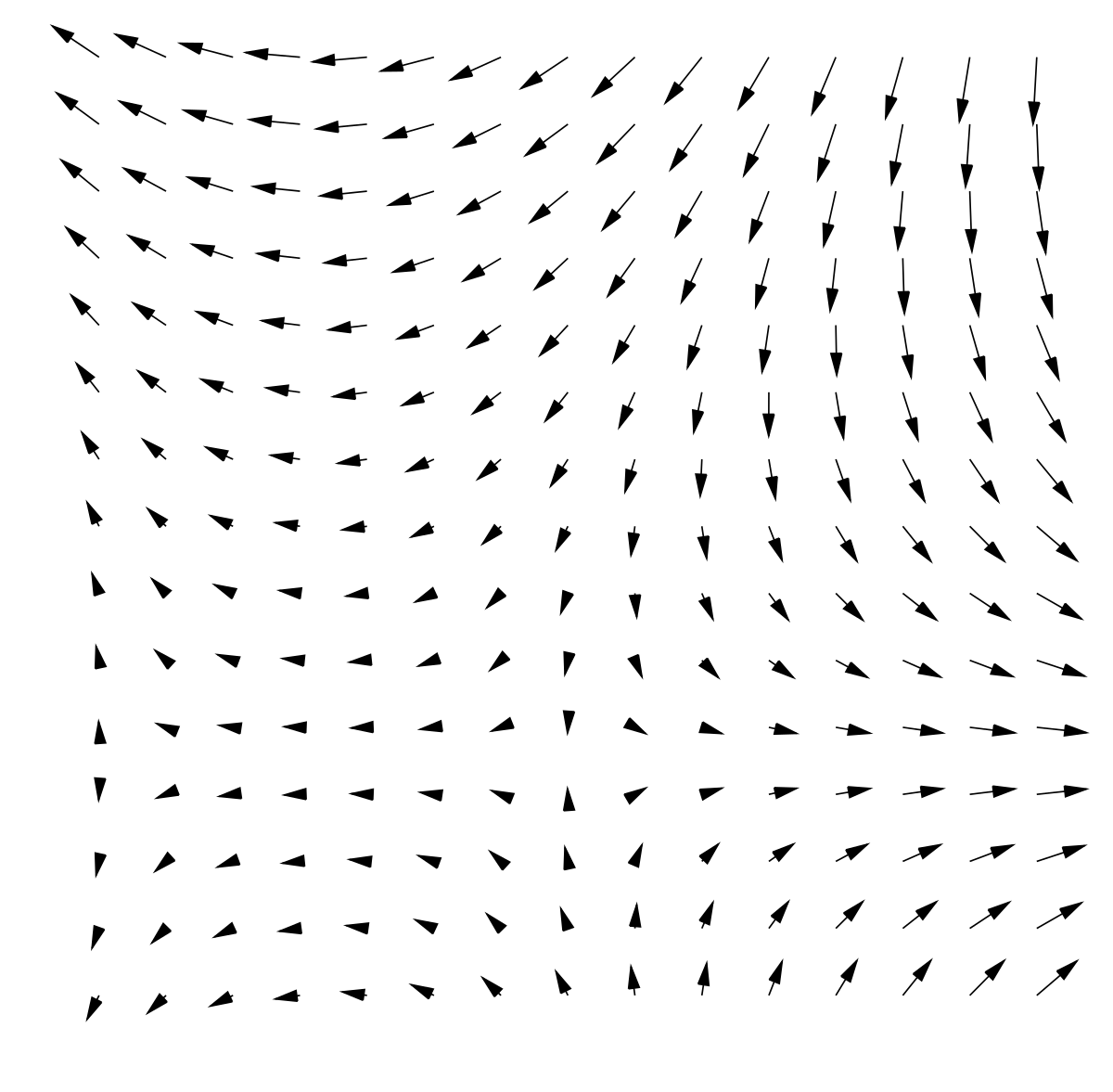
En mathématiques, un champ de vecteurs ou champ vectoriel est une fonction qui associe un vecteur à chaque point d'un espace euclidien ou plus généralement d'une variété différentielle.
Les champs de vecteurs sont souvent utilisés en physique, pour modéliser par exemple la vitesse et la direction d'un fluide en mouvement dans l'espace, ou la valeur et la direction d'une force, comme la force magnétique ou gravitationnelle, qui évoluent points par points.
Notion mathématique
Soit E un espace vectoriel euclidien et U un ouvert de E. Un champ de vecteurs de classe de régularité Ck sur U est une application F de classe Ck de U dans E, définie par ses n fonctions composantes :
Exemples :
- les vecteurs du repère mobile des coordonnées polaires ;
- le vecteur position.
Champ de gradient
Un champ de vecteurs X est appelé champ de gradient quand il existe une fonction f telle qu'en tout point, X est le gradient de f. On dit encore que X dérive du potentiel f. Dans ce cas, les différents potentiels diffèrent d'une constante.
Dans le plan, si le champ de vecteurs X dérive d'un potentiel f, les lignes de niveau de f, courbes sur lesquelles f est égale à une constante, sont appelées courbes équipotentielles pour le champ de vecteurs. En tout point où le champ est non nul, il est normal aux courbes équipotentielles.
Si le champ de vecteurs est tracé sur un ouvert de l'espace à trois dimensions, on parle de même de surfaces équipotentielles. Plus généralement, en dimension quelconque, on a affaire à des hypersurfaces équipotentielles, auxquelles le champ de vecteurs est normal.
Dans l'espace à trois dimensions, un champ de gradient a toujours un rotationnel nul. La réciproque fait intervenir la topologie de l'ouvert U : si U est simplement connexe, un champ de vecteurs est un champ de gradient si et seulement si son rotationnnel est nul.
Circulation le long d'un chemin
La notion de circulation est utilisée notamment en physique pour le calcul du travail d'une force.
Soit γ un chemin tracé sur l'ouvert U, c'est-à-dire un arc paramétré de [a,b] dans U, de classe
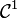
Cette valeur est invariante par changement de paramétrage.
Si le champ dérive d'un gradient f, la circulation ne dépend que des extrémités du chemin
Elle est notamment nulle sur tout lacet (chemin fermé).
Dualité avec les formes différentielles
Une forme différentielle de degré un et de classe


En effet, l'espace étant euclidien, le produit scalaire permet de définir un isomorphisme entre E et son dual. Si X est un champ de vecteurs sur U, on peut lui associer la forme différentielle définie en chaque point par
et cette association est une bijection entre champs de vecteurs et formes différentielles d'ordre 1.
En conséquence l'analogie entre les théorèmes concernant formes différentielles et champs de vecteurs n'est pas surprenante : voici un tableau de correspondance.
| Champ de vecteurs | Forme différentielle d'ordre 1 |
|---|---|
| Circulation | Intégrale curviligne |
| Champ de gradient | Forme différentielle exacte |
| Rotationnel (dim 3) | Dérivée extérieure |
| Rotationnel nul (dim 3) | Forme différentielle fermée |
Remarque : on peut étendre la notion de rotationnel à des dimensions autres que 3.
Courbes intégrales d'un champ de vecteurs, lignes de champ
Au champ de vecteurs X tracé sur l'ouvert U, on peut associer l'équation différentielle γ' = X(γ). Les fonctions solutions sont les arcs paramétrés γ de classe
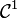
C'est-à-dire que le vecteur dérivé en chaque point est donné par le champ en ce point.
Les solutions maximales de cette équation différentielle sont appelées courbes intégrales du champ de vecteurs. Elles sont tangentes en chaque point au champ de vecteurs. Dans le cas d'un champ de gradient, elles sont donc orthogonales aux lignes ou surfaces de niveau. La fonction qui à t, x associe le point qui était en position x à l'instant 0 est appelée le flot de l'équation différentielle.
Le théorème de Cauchy-Lipschitz assure l'existence et l'unicité d'une solution maximale pour chaque couple de conditions initiales (t0,x0). Il s'appliquerait même si le champ était seulement une fonction lipschitzienne.