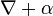Connexion de Koszul - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En géométrie différentielle, une connexion (de Koszul) est un opérateur sur les sections d'un fibré vectoriel. Cette notion a été introduite par Koszul en 1950 et formalise le transport parallèle de vecteurs le long d'une courbe en termes d'équation différentielle ordinaire. Les connexions sont des objets localement définis auxquels sont associés les notions de courbure et de torsion. L'un des exemples les plus simples de connexions de Koszul sans torsion est la connexion de Levi-Civita naturellement définie sur le fibré tangent de toute variété riemannienne.
L'ensemble des connexions de Koszul forme un espace affine réel dont l'espace directeur est l'espace des 1-formes différentielles de B à valeurs dans End(E), le fibré vectoriel des endomorphismes de E. Une connexion sur E induit des connexions sur les fibrés construits à partir de E par des opérations algébriques élémentaires (produit extérieur, produit tensoriel, ...). L'utilisation des connexions permet en particulier d'effectuer un calcul différentiel extérieur raisonnable sur les sections de E. Elles sont fortement utilisées en analyse.
Définitions
Soit E l'espace total d'un fibré vectoriel réel de rang fini de base B variété différentielle réelle. À une section globale s de E et un champ de vecteurs X de B est associée une section notée
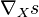
- Linéarité en X : Pour toute fonction différentiable f, et pour tout champ de vecteur X de B, on a :
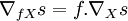
- Règle de Leibniz : Pour toute fonction différentiable f et pour tout champ de vecteur X de B, on a :
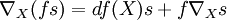
La première propriété implique en particulier que la valeur de
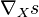
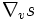

Exemple
Les sections d'un fibré trivial
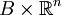
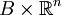
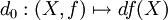
Naturellement, les connexions de Koszul se transportent par isomorphisme de fibrés vectoriels (on reviendra sur ce point). En particulier tout fibré trivialisable admet des connexions de Koszul. Cependant, cette connexion dépend de la trivialisation choisie.
Un groupe de Lie G est parallélisable et admet donc des connexions de Koszul. Plus exactement, le choix d'une base de l'espace tangent en l'élément neutre induit par translation à gauche une trivialisation de TG ; on dispose donc d'une connexion de Koszul D0 définie comme ci-dessus. Cette connexion ne dépend du choix de la base.
L'existence de connexions sur un fibré quelconque s'appuie sur un argument de partitions de l'unité. En supposant B dénombrable à l'infini, B admet un recouvrement localement fini {Ui} au plus dénombrable d'ouverts localement compacts au-dessus desquels le fibré E est trivialisable. Il existe une partition de l'unité {fi}, le support de fi étant inclus dans Ui. En particulier, au-dessus de Ui, il existe une connexion
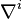
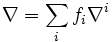
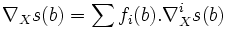
Comme la somme des fi vaut 1,

Définitions équivalentes
Selon les auteurs, la définition d'une connexion de Koszul admet de légères variantes. Si Γ(E) désigne l'espace vectoriel des sections de E, une connexion

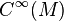
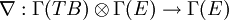
Autre interprétation possible, pour toute section s de E,
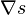

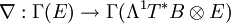
La règle de Leibniz se traduit alors ainsi : pour toute fonction differentiable f et pour toute section s de E,
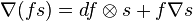
En outre, les connexions de Koszul peuvent se définir de manière analogue sur les fibrés vectoriels complexes, en prenant en compte que l'espace des sections est un module sur l'algèbre des fonctions différentiables non plus réelles mais complexes. La seule différence est donc de tenir compte des fonctions différentiables complexes dans la règle de Leibniz.
Structure affine
Si
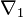
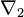
![\nabla^2(fs)=df\otimes s +f\nabla^2s=\nabla^1(fs)+f\left[\nabla^2-\nabla^1\right] s](https://static.techno-science.net/illustration/Definitions/autres/e/e34509172c06b417b53b299d30747e9e_b9c25d242a87a0f49bc78eab5d25a82b.png)
Leur différence
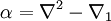
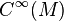

L'ensemble des connexions de Koszul sur E est alors naturellement un espace affine d'espace directeur l'espace des 1-formes differentielles à valeurs dans End(E). L'action du groupe G(E) est affine. Plus exactement, pour tout automorphisme g de E, on a :
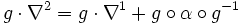
En particulier, dans une trivialisation locale de E donnée par un isomorphisme Φ de fibres au-dessus de U de
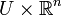

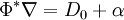
où α est une 1-forme differentielle à valeurs matricielles.
Courbure
La courbure de

![R(X,Y)s=\nabla_X\nabla_Ys-\nabla_Y\nabla_Xs -\nabla_{[X,Y]}s](https://static.techno-science.net/illustration/Definitions/autres/e/e3ec074f2d96e31bc3d3c84e96768dfd_9db9ec4769eb554458f4150b7fd9de0c.png)
Dans une trivialisation locale, en reprenant les notations ci-dessus, si
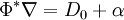
où par convention:
D'autres notions de courbures pour les connexions de Koszul existent mais elles dépendent de structures supplémentaires.
Torsion
Pour une connexion de Koszul

![T(X,Y)=\nabla_XY-\nabla_YX-[X,Y]](https://static.techno-science.net/illustration/Definitions/autres/a/a193fb16fdcadc1be25dea16473d4f43_ec53c111d59c6da127ec43fff69173a5.png)
Le fait que T soit effectivement un tenseur demande vérification. Une connexion est dite sans torsion lorsque sa torsion est nulle. Si α est une 1-forme différentielle à valeurs dans End(TM), et que