Variété riemannienne - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en géométrie, une variété riemannienne est une variété différentielle ayant une structure supplémentaire (une métrique) permettant de définir la longueur d'un chemin entre deux points de la variété.
Définitions et exemples élémentaires
Définition formelle
Une variété riemannienne est la donnée d'une variété différentielle M et, en chaque point m, d'une forme quadratique définie positive gm sur l'espace tangent Tm avec des hypothèses de régularité supplémentaires. Les espaces tangents (TmM,gm) sont des espaces euclidiens. Les hypothèses de régularité s'énoncent de deux manières équivalentes :
- L'application
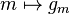
- Pour tout champ de vecteurs X,Y de M, l'application
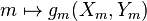
La donnée g est appelée métrique riemannienne sur M. Les métriques riemanniennes existent sur toute variété différentielle (paracompacte) et forment un cône convexe fermé de ΓS2T * M (avec des topologies raisonnables).
Si (M,g1) et (N,g2) sont deux variétés riemanniennes, une isométrie locale
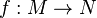
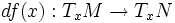
Une isométrie est un difféomorphisme et une isométrie locale.
Longueur et distance.
Les variétés riemanniennes sont les exemples les plus élémentaires de variétés de Finsler. Une métrique riemannienne g sur une variété différentielle connexe M définit sur chaque espace tangent une norme (de Banach), donnée par :
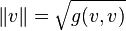
Par définition, la longueur d'une courbe C1 par morceaux γ: [a, b] → M est définie par :
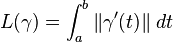
- La longueur d'une courbe est invariante par reparamétrage régulier.
- La longueur du concaténé de deux courbes C1 par morceaux est la somme des longueurs.
Pour
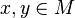
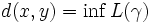
où l'infinimum porte sur toutes les courbes C1 par morceaux d'origine x et d'extrémité y.
Comme les notations le laissent suggérer, d est une distance sur M appelée distance riemannienne. Il est à remarquer que cette dernière redéfinit la topologie de M.
Exemples fondamentaux
Les sphères
L'espace hyperbolique
Disque de Poincaré : L'espace hyperbolique (Hn,g) est le disque unité de

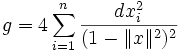
Demi-plan de Poincaré : Ce modèle du plan hyperbolique est donné par la métrique définie sur le demi-plan supérieur
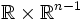
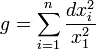
Une isométrie explicite du disque unité sur le demi-plan supérieur est donnée par l'inversion de pôle
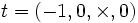
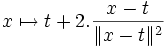
Remarque : L'espace hyperbolique H2 intervient en arithmétique, domaine dans lequel on utilise habituellement le modèle du demi-plan supérieur. Toutefois, en géométrie, les goûts sont très largement partagés : le modèle du disque de Poincaré offre l'avantage d'un meilleur graphisme dans les figures. Il existe d'autres modèles (comme le modèle de l'hyperboloïde), peu utilisés en pratique.
Se référer à la géométrie hyperbolique pour un exposé plus complet sur le sujet.
Courbure
Courbure sectionnelle
Courbure et topologie
De la connexion aux géodésiques
Connexion de Levi-Civita
Sur une variété riemannienne (M,g), il existe une unique connexion sans torsion telle que, pour tout champ de vecteurs X,Y,Z :
Cette connexion est appelée la connexion de Levi-Civita de (M,g), ou la connexion canonique.
Si
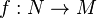
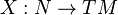
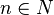
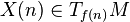
![\Gamma\left[f^*TM\right]](https://static.techno-science.net/illustration/Definitions/autres/f/f9c47f67928ec84c224180e5ac0bf0b4_fb646bfb90558e8b3d8100ced860a7cb.png)
Équations des géodésiques
![\frac{d^2x^i}{dt^2}+\sum \Gamma^i_{jk}\left[c(t)\right]\frac{dx^k}{dt}\frac{dx^l}{dt}=0](https://static.techno-science.net/illustration/Definitions/autres/6/6c56db1789ca83476ca8920fb5bbe8d7_717409125d822a102dca62d94c068657.png)
Théorème de Hopf-Rinow
Les propriétés suivantes sont équivalentes :
- Pour tout point m, l'application expm est définie sur TmM
- La variété (M,g) est géodésiquement complète, ie : les géodésiques sont définies sur

- L'espace M est complet pour la distance riemannienne.
- Les boules fermées et bornées sont compactes.

















































