Constantes mathématiques (représentées en fraction continuée) - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Voici une table de constantes mathématiques exprimées par leurs notations et par leurs représentations en fraction continue :
(Constantes connues comme étant irrationnelles avec un développement en fraction continue infini : leur dernier terme est ....)
| Nom | Ensemble de nombres | Définition ou valeur approchée | Représentations en fraction continue |
|---|---|---|---|
| Λ |
| > – 2,7 · 10-9 | |
|
|
|
|
|
| 1/2 |
|
|
|
| C2 |
| |
![C_2= [0; 1, 1, 1, 16, 2, 2, 2, 2, 1, 18, 2, 2, 11, 1, 1, 2, 4, 1, 16, 3, 2, 4, 21, 2, 405, 2, 1, 33, 1, 1] = 0 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/d/de16dd722910e59af11677c9463ced90_6c7b7bd0da3f923a204a07cb24822939.png)
|
| γ |
|
|
![\gamma = [0; 1, 1, 2, 1, 2, 1, 4, 3, 13, 5, 1, 1, 8, 1, 2, 4, 1, 1, 40, 1, 11, 3, 7, 1, 7, 1, 1, 5, 1, 49, ...] = 0 + \frac{1}{1 + \frac{1}{1 + \frac{2}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/b/bc82cec452c072a32b2ed4c5a4d5513e_63d0d4f7593e807e4ce053e5d44205e1.png)
|
| β* |
|
|
![\beta^{*} = [0; 1, 2, 2, 1, 3, 5, 1, 2, 6, 1, 1, 5] = 0 + \frac{1}{1 + \frac{2}{1 + \frac{2}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/8/8ec84afcca5ae1c31ece60642dbaacd2_a501a97c288a84aa849de0ac7f60d77c.png)
|
| K |
|
|
![K = [0; 1, 3, 4, 6, 1, 15, 1, 2, 2, 3, 1, 23, 3, 1, 1, 3, 1, 1, 7, 2, 3, 3, 18, 2, 1, 2, 1, 2, 1, 6] = 0 + \frac{1}{1 + \frac{3}{1 + \frac{4}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/b/bf5e8b51f5f0afdd842400b4b6a161f2_365c16a1d412ab7374fe2f09daaae2ed.png)
|
| B4 |
| |
![B_4 = [0; 1, 6, 1, 2, 1, 2, 956, 8, 1, 1, 1, 23] = 0 + \frac{1}{1 + \frac{6}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/1/19fce12d6b2bc314fc351e35714098c0_10a10e18d0f2c91c02c639dbdd73b77f.png)
|
| K |
| |
![K = [0; 1, 10, 1, 8, 1, 88, 4, 1, 1, 7, 22, 1, 2, 3, 26, 1, 11, 1, 10, 1, 9, 3, 1, 1, 1, 1, 1, 1, 2, 2] = 0 + \frac{1}{1 + \frac{10}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/0/0b051c195c56650c29a98958a5142ee5_9373683f3c1a93a6ba0ca5689c4a308a.png)
|
| M1 |
| |
![M_1= [0; 3, 1, 4, 1, 2, 5, 2, 1, 1, 1, 1, 13, 4, 2, 4, 2, 1, 33, 296, 2, 1, 5, 19, 1, 5, 1, 1, 1, 1, 1] = 0 + \frac{3}{1 + \frac{1}{1 + \frac{4}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/f/ff4e62fa2263868c07f6e7ed991a664b_d2b7239c4d7d2df7186f3cbbe288c57c.png)
|
|
|
|
| [1;] |
| Nombre d'or (phi) |
| |
![\phi = [1; 1, 1, 1, ...] = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/5/545cfcd18fedb86cb00f8dd8137ed54d_f2fb93309b7136de0aac6366224863e4.png)
|
| EB |
|
|
![E_B = [1; 1, 1, 1, 1, 5, 2, 1, 2, 29, 4, 1, 2, 2, 2, 2, 6, 1, 7, 1, 6, 2, 1, 1, 1, 20, 1, 3, 1, 1, 1, ...] = 1 + \frac{1}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/6/6948d9347360f7c0c577258ca75213a2_f2ea0966f87149011ff9711d196612b1.png)
|
| B2 |
| |
![B_2 = [1; 1, 9, 4, 1, 1, 8, 3, 4, 7, 1, 3, 3, 1, 2, 1, 1, 12, 4, 2, 1, 2, 2] = 1 + \frac{1}{1 + \frac{9}{1 + \frac{4}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/0/06304217ffce109b6c86f45e0504b19a_a2b5a72d2becb6408b0e00de8322607c.png)
|
| K |
|
|
![K = [1; 7, 1, 1, 2, 1, 3, 2, 1, 2, 1, 17, 1, 1, 2, 1, 2, 4, 1, 2] = 1 + \frac{7}{1 + \frac{1}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/b/b5783926658b7e318222605982760c2c_d0c4cf30158e4052902ee507b8c75c58.png)
|
| √2 |
| |
![\sqrt{2} = [1; 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, 2, ...] = 1 + \frac{2}{1 + \frac{2}{1 + \frac{2}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/a/aa76f5b91e4131081ec67ca269da7407_17246cf19c8020dea3fab8c0def4f697.png)
|
| μ |
| Unique zéro positif de la fonction |
![\mu = [1; 2, 4, 1, 1, 1, 3, 1, 1, 1, 2, 47, 2, 4, 1, 12, 1, 1, 2, 2, 1, 7, 2, 1, 1, 1, 2, 30, 6, 3, 6] = 1 + \frac{2}{1 + \frac{4}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/5/52f392f552a06c296150a38186d5c2ec_de19e34cead18bc1f94936bc3ba94985.png)
|
|
|
|
|
|
| α |
| ≈ 2,502 907 875 095 892 822 283 902 873 218 215 78 |
![\alpha = [2; 1, 1, 85, 2, 8, 1, 10, 16, 3, 8, 9, 2, 1, 40, 1, 2, 3, 2, 2, 1, 17, 1, 1, 5, 3, 2, 6, 3, 5, 1] = 2 + \frac{1}{1 + \frac{1}{1 + \frac{85}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/5/5ec873fc3ccf4b20bab5be2fbd4bea14_47dcd405679e6505b8ad096109ec273a.png)
|
| e |
| |
![e = [2; 1, 2, 1, 1, 4, 1, 1, 6, 1, 1, 8, 1, 1, 10, 1, 1, 12, 1, 1, 14, 1, 1, 16, 1, 1, 18, 1, 1, 20, 1, ...] = 2 + \frac{1}{1 + \frac{2}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/c/c75b68077979560737422168cf24193d_4958b823fe3d9bfa85ca05d65730a924.png)
|
| Kh |
| Pour :
|
![K_h = [2; 1, 2, 5, 1, 1, 2, 1, 1, 3, 10, 2, 1, 3, 2, 24, 1, 3, 2, 3, 1, 1, 1, 90] = 2 + \frac{1}{1 + \frac{2}{1 + \frac{5}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/5/504b7bcc9a93327488354fbbe1e08261_cb6976f56a608ed7e70490d3f4965eb4.png)
|
| 3 |
|
|
|
| π |
|
|
![\pi = [3; 7, 15, 1, 292, 1, 1, 1, 2, 1, 3, 1, 14, 2, 1, 1, 2, 2, 2, 2, 1, 84, 2, 1, 1, 15, 3, 13, 1, 4, 2, ...] = 3 + \frac{7}{1 + \frac{15}{1 + \frac{1}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/e/e6a97d7b209126c8c8fe13eb1846b658_dee92fba9269320e04bc159b1c4186fb.png)
|
| 4 |
|
|
|
| δ |
| ≈ 4,669 201 609 102 990 671 853 203 820 466 201 61 |
![\delta = [4; 1, 2, 43, 2, 163, 2, 3, 1, 1, 2, 5, 1, 2, 3, 80, 2, 5, 2, 1, 1, 1, 33, 1, 1, 53, 1, 1, 1, 1, 1] = 4 + \frac{1}{1 + \frac{2}{1 + \frac{43}{1 + \cdots}}}](https://static.techno-science.net/illustration/Definitions/autres/c/cf9e8d4aef5d6fc07ab3dd2160b8c0a6_340de069508a2a9e3304ccc34eb3acf6.png)
|
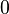

![[0;]\,\!](https://static.techno-science.net/illustration/Definitions/autres/9/935b904604aa062eeb36c57356ea2014_62a25daa340c615d8571597028e6fdba.png)

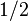
![[0; 2]\,\!](https://static.techno-science.net/illustration/Definitions/autres/d/d0a654f93b63022dd93bcb52cc8fe8c9_31f0bf26473c5936338f3c370f24a0d4.png)
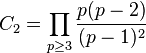
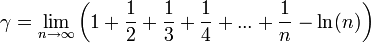
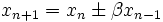
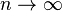
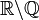
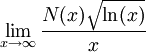
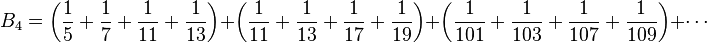
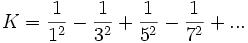
![M = \lim_{n \rightarrow \infty } \left( \sum_{p \leq n} \frac{1}{p} - \ln(\ln(n)) \right)=\gamma + \sum_{p} \left[ \ln \left( 1 - \frac{1}{p} \right) + \frac{1}{p} \right]](https://static.techno-science.net/illustration/Definitions/autres/5/5e64515f3b653026f658bf6cdc98834a_b1bb60be5d87e64f929a3d34596308e5.png)
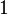
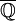
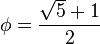
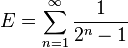
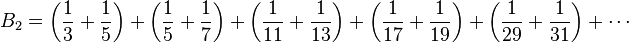
![\sqrt[n]{|f_n|} \to 1,13198824\dots \mbox{quand }n \to \infty.](https://static.techno-science.net/illustration/Definitions/autres/6/6e3c091ca34c64c6f20b8fd7c3b4653d_38d128a09d018f4c1b7ae54aef4c3429.png)
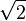
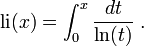
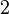
![[2;]\,\!](https://static.techno-science.net/illustration/Definitions/autres/5/53beffacdfe66522dcd5dde82938178d_0a0e7bc012ca0e109114dd14d29c1bf6.png)
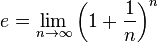
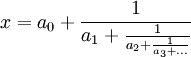
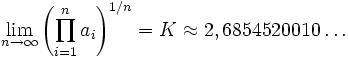
![[3;]\,\!](https://static.techno-science.net/illustration/Definitions/autres/8/8374d111f8e965b5c02bf508d79c887a_0be318172b67293a6b0c001c509dd1f1.png)
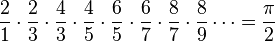
![[4;]\,\!](https://static.techno-science.net/illustration/Definitions/autres/2/2bf4485a6d4c8c4d62572aae7f585284_9d2de1bbc1103303c6acac76f98f4a30.png)

















































