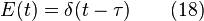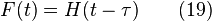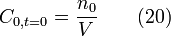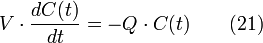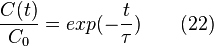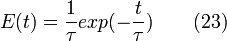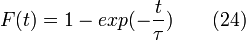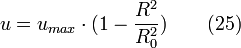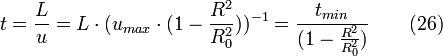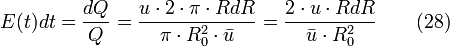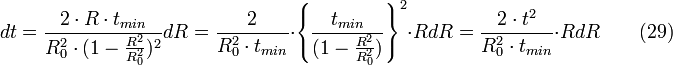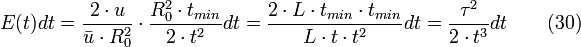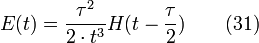Distribution de temps de séjour - Définition

DTS des réacteurs idéaux

Réacteur tubulaire idéal

Le réacteur tubulaire idéal n'a qu'une fonction retardatrice et ne change pas le signal d'entrée. Pour une injection par impulsion, on obtient le même signal à la sortie après un certain temps qui correspond au temps de séjour moyen τ.

La distribution de séjour est un pic très étroit situé au temps τ.

Le même raisonnement peut être appliqué à l'injection échelon où l'on obtient un échelon décalé de τ avec une réponse désignée par

où H est la fonction échelon unité de Heaviside.

Réacteur parfaitement mélangé

Si l'on introduit dans un réacteur parfaitement mélangé une impulsion de n₀ moles de traceur, le système va instantanément atteindre la concentration moyenne maximale

L'évolution de la concentration en fonction du temps peut alors être déduite par l'intégration du bilan de matière donné par l'équation (21) où la variation de la quantité de traceur dans le réacteur est égale à la quantité de traceur qui quitte le réacteur :

ce qui donne

d'où

Réacteur tubulaire à écoulement laminaire

Le réacteur tubulaire à écoulement laminaire est un cas particulier du réacteur tubulaire avec un comportement hydrodynamique connu et bien défini, ce qui permet d'en prédire la distribution de séjour. La différence de temps de séjour des éléments de volume dans le réacteur est la conséquence du profil de vitesse parabolique (Ecoulement de Poiseuille). Dans un filet de fluide de position radiale constante, chaque particule traverse le réacteur sans être influencée par les autres.

La vitesse dans un tube ayant un écoulement laminaire est fonction de la position dans le tube

où u_max est la vitesse au centre du tube et la valeur moyenne sur la section . La relation entre ces 2 vitesses est .

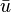
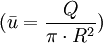
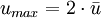
Le temps de séjour d'un élément de volume qui se trouve dans un filet de fluide donné vaut ainsi:

avec

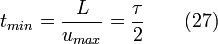
La fraction du flux qui se trouve dans la position R + dR avec une vitesse v + dv qui a un temps de passage t + dt se calcule avec la relation suivante:

Pour obtenir la relation entre dt et dR, on utilise l'équation (27) et par dérivation, on a

Et en utilisant la dérivée (29) et la relation (22), on peut simplifier l'équation (23)

En incluant la fonction retardatrice du réacteur piston et en observant que le plus petit temps de séjour possible est donnée par l'équation (22), on a finalement