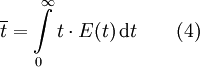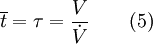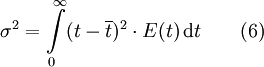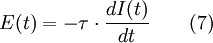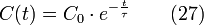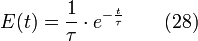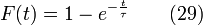Distribution de temps de séjour - Définition

Théorie

Figure 1: Exemple de distribution de fréquence pour un réacteur continu

Pour caractériser l'écoulement, on utilise dès lors la distribution de temps de séjour qui est une approche statistique. En effet, on considère un élément du fluide à son entrée dans le réacteur et on mesure le temps que ce dernier met pour atteindre la sortie. Si on répète l'expérience ou on considère plusieurs éléments en même temps, on constatera que les résultats ne sont pas identiques. Les causes principales de cette différence est l'existence de zones stagnantes ou de court-circuits dans l'installation étudiée. On peut dès lors établir une distribution des temps de séjour, le plus souvent représentée par une distribution de fréquences appelée habituellement E. Pour ce faire, quatre hypothèses sont posées:

• le réacteur est à l'état stationnaire
• le fluide est incompressible
• à l'entrée et à la sortie du réacteur, le transport a lieu uniquement par convection et est de type piston
• le diamètre de l'entrée et de la sortie des flux est petit par rapport au diamètre du réacteur

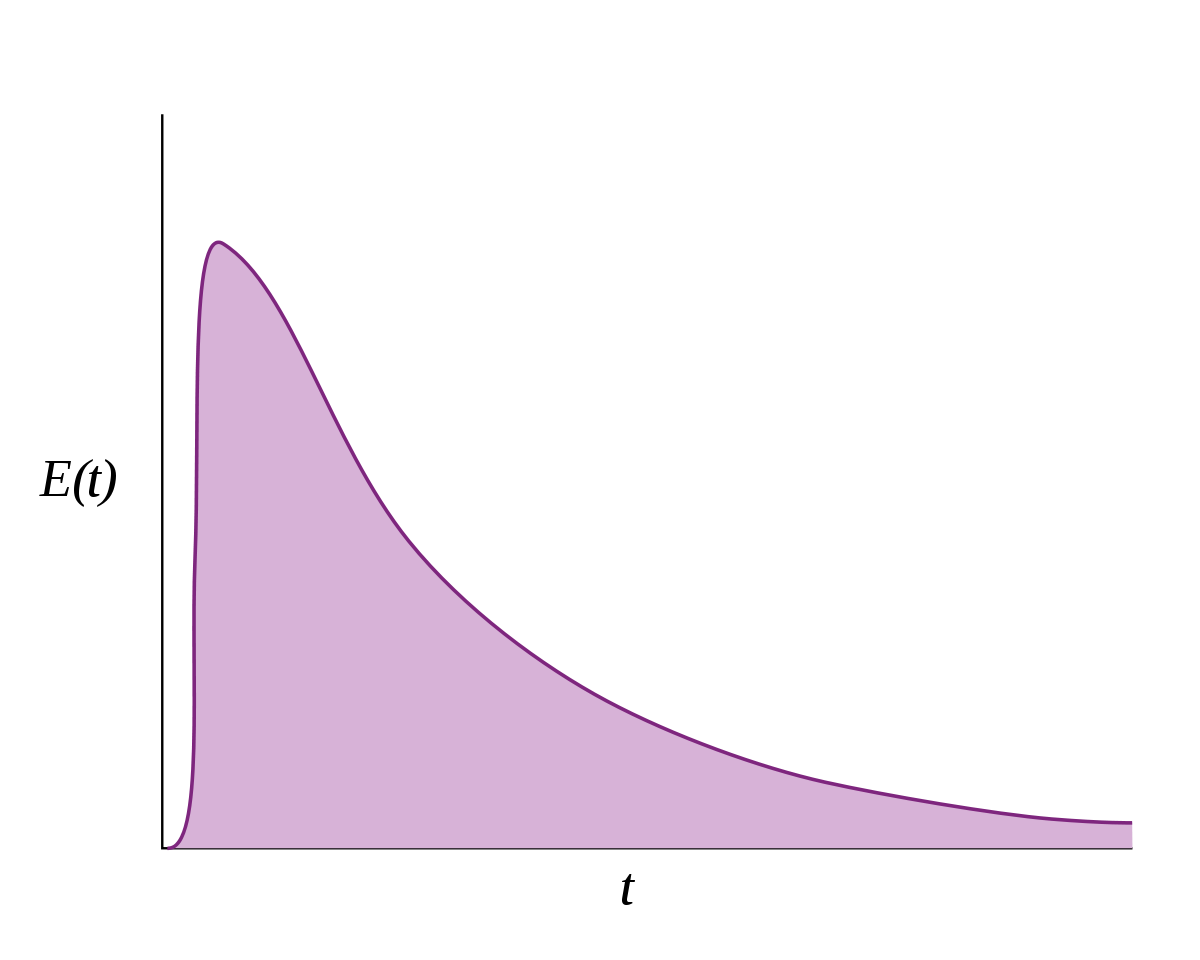
Dans ces conditions, la fonction E rapporte l'âge des éléments qui quittent le réacteur à un moment donné. La dimension E(t) correspond ainsi à une fraction du flux total ayant un certain âge par unité de temps.
La fraction du fluide qui séjourne durant un intervalle de temps donné dans le système est donné par la valeur E(t)•Δt (cf. Figure 1).

Les relations suivantes peuvent être définies:

   fraction du fluide qui quitte le réacteur avec un âge plus jeune que t₁

   fraction du fluide qui quitte le réacteur avec un âge plus âgée que t₁

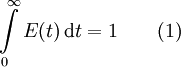
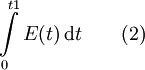
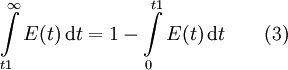
La moyenne de la distribution, qui correspond à la moyenne des temps de séjour, est donnée par le premier moment de la distribution

La moyenne des temps de séjour est égale au temps de passage si la densité du système est constante

Les moments centrés d'ordre supérieur à 1 fournissent des informations non-négligeables sur le comportement de la fonction E(t). Par exemple, le moment centré d'ordre 2 indique la dispersion autour de la moyenne, c.-à-d. la variance.

Le moment centré d'ordre 3 indique l'asymétrie de la fonction E(t) et celui d'ordre 4 l'aplatissement de cette dernière.

On peut également définir une distribution d'âge interne, nommée I(t), pour le contenu du réacteur. Cette valeur possède la même définition que E(t): il s'agit de la fraction du flux total au sein du réacteur ayant un certain âge par unité de temps. La relation qui relie E(t) et I(t) est donnée par

Modèles des réacteurs réels

Les réacteurs réels présentent des déviations plus ou moins importantes par rapport aux modèles. Ceci peut poser des problèmes pour le dimensionnement des réacteurs ou l'optimisation des conditions opératoires. Pour identifier ces déviations, une comparaison de la distribution de temps de séjour d'un réacteur avec les modèles est nécessaire et permet de définir les modifications à apporter pour corriger la non-idéalité ou pour apporter un facteur de correction pour les calculs de dimensionnement.

On distingue 2 grandes causes de déviations: les zones mortes, espaces du réacteur dont le contenu ne se mélange pas ou très peu avec le flux traversant le réacteur, et les court-circuits, canaux ou chemins qui permettent au flux de traverser le réacteur sans se mélanger au contenu du réacteur.

Détection des non-idéalités pour le réacteur continu

• a) Cas idéal

Distribution de temps de séjour idéale pour une impulsion dans un réacteur continu

Dans un cas idéal avec un liquide incompressible, le temps de passage τ est défini par la relation habituelle



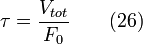
Ceci permet de définir les différentes courbes caractéristiques d'une impulsion par les équation suivantes

• b) Cas avec court-circuit

Distribution de temps de séjour pour une impulsion dans un réacteur continu avec un court-circuit

Dans le cas d'un court-circuit, une partie du traceur ne se mélange pas avec le mélange réactionnel présent en début d'expérience dans le réacteur et est directement évacuée vers la sortie. On peut représenter ce problème par une division du flux d'entrée en 2 parties: une entrant dans le réacteur et se mélangeant au contenu de ce dernier, la seconde étant directement déviée vers le flux de sortie sans passer dans le réacteur.



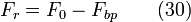
Le temps de passage sera donc plus grand que celui d'un réacteur idéal et la fonction E(t) diminuera moins rapidement que dans le cas du réacteur idéal. La fonction E(t) peut être modélisée par l'équation suivante qui intègre le court-circuit comme étant un tube parallèle au réacteur et qui peut être représenter comme un réacteur tubulaire.



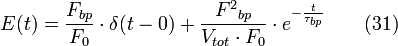
On constate pour la fonction F(t) un seuil qui est formé par le court-circuit.

• c) Cas avec zone morte

Distribution de temps de séjour pour une impulsion dans un réacteur continu avec un volume mort

Dans le cas d'un volume mort, le volume réel de mélange dans le réacteur est réduit par rapport au cas idéal: il s'agit de zones où la circulation induite par mouvement de l'agitateur est nulle. Pratiquement ces zones ne participent pas au mélange et sont considérées comme mortes.



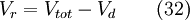
Le temps de passage sera donc plus petit que celui d'un réacteur idéal et la fonction E(t) diminuera plus rapidement que dans le cas du réacteur idéal.

Détection des non-idéalités pour le réacteur tubulaire

Théoriquement le réacteur tubulaire ne modifie pas le signal, il ne fait que le retarder.

• a) Cas idéal

• b) Cas avec court-circuit

• c) Cas avec zone morte