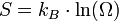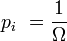Ensemble microcanonique - Définition

Introduction

En physique statistique, l'ensemble microcanonique est l'ensemble des répliques fictives d'un système réel dont l'énergie (E), le volume (V) et le nombre de particule (N) sont fixés. Cet ensemble statistique a une importance particulière, car c'est à partir de celui-ci que le postulat de la physique statistique est défini. Cet ensemble permet aussi de déterminer les ensembles canonique et grand-canonique, à l'aide d'échange d'énergie ou de particules avec un réservoir.

Introduction

Du point de vue de la mécanique quantique, la connaissance la plus complète que l'on puisse obtenir d'un système est la connaissance de sa fonction d'onde qui est fonction des coordonnées de chacune des molécules du système. Cette fonction d'onde est solution de l'équation de Schrödinger que l'on peut écrire de manière condensée sous la forme

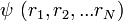
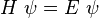
La connaissance de la composition N du système permet d'exprimer l'opérateur hamiltonien , la connaissance de V précise les conditions aux limites auxquelles doit satisfaire . Dans ce cas, la connaissance de l'énergie du système (E), valeur propre de l'équation, permet d'écrire la liste complète de toutes les fonctions propres .

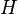
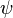
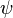
Entropie

Dans l'ensemble microcanonique, l'entropie statistique a été défini par Boltzmann par la relation :

où

• k_B = 1,381.10 ^{− 23}J.K ^{− 1} s'appelle la constante de Boltzmann,
• est le nombre d'état microscopique du système.

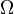
Hypothèses

Le système considéré est isolé et composé de N objets microscopique identiques pouvant être des atomes, des molécules, des spins, etc...

Nombre d'état microscopique

Le nombre total de solution de l'equation de Schrödinger est noté . Ce nombre représente mathématiquement la dimension vectorielle des solutions de l'équation de Schrödinger, et il dépend des variables qui déterminent l'état macroscopique du système. Chaque état microscopique possède, pour un état macroscopique défini, la même énergie E, le même nombre de particules N, et le même volume V.

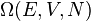
Postulat

Le postulat de la physique statistique précise pour un système isolé (E, V, N fixés) :

c'est-à-dire les états correspondant aux fonctions d'onde du système sont également probable.

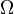
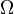
Si on note p_i la probabilité associé à chaque micro-état i, on obtient alors :

Mesure d'une grandeur

Sur base de ce qui est dit plus haut, le sens de la mesure d'une grandeur quelconque du système a alors le sens suivant : pendant le temps t que dure la mesure, le système évolue en passant d'un état microscopique (une réplique) à une autre. Toute mesure effectuée est nécessairement une moyenne sur le temps des différents états traversés.

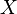
Dans le cas d'un système réel, la fonction d'onde dépend du temps. A tout instant i, on peut, en quelque sorte, « photographier » le système dans un état microscopique particulier, c'est-à-dire en avoir une réplique particulière (représentée par la fonction d'onde , solution de l'équation de Schrodïnger). Or nous possédons théoriquement la liste des fonctions d'onde permises et nous connaissons donc tous les états microscopiques par lesquels le système est susceptible de passer.

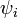
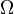
En résumé, la fonction d'onde totale solution du système réel, est équivalente à un ensemble de fonctions d'onde réplique du système dans chacun des états particuliers qu'il est susceptible d'occuper

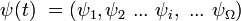
Supposons maintenant la mesure de la grandeur . Sur base du postulat, et en considérant un ensemble de réplique d'un système où chaque réplique figure en un même nombre d'exemplaire (par exemple, une fois chacune), la valeur de la grandeur dans chaque réplique sera notée :

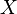
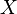
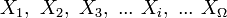
La moyenne de cette grandeur calculée avec l'ensemble des répliques est alors la somme (sur tous les états microscopiques du système considéré) de la probabilité d'être dans l'état i multiplié par la valeur X_i de cet état :

D'après l'hypothèse ergodique, cette moyenne doit coincider avec la valeur moyenne mesurée sur le système réel et est définie par