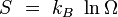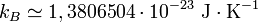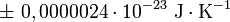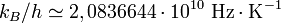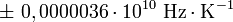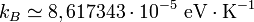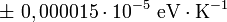Constante de Boltzmann - Définition

Introduction

La constante de Boltzmann k (ou k) a été introduite par Ludwig Boltzmann lors de sa définition de l'entropie en 1873. Le système étant à l'équilibre macroscopique, mais libre d'évoluer à l'échelle microscopique entre Ω micro-états différents, son entropie S est donnée par :

Cette constante physique fondamentale est égale à R / N

• R est la constante des gaz parfaits : R = 8,314 J⋅K^-1⋅mol^-1

• N est le nombre d'Avogadro égal à N = 6,022×10²³ mol^-1

d'où k ≈ 1,380×10^-23 J⋅K^-1

k peut s'interpréter comme le facteur de proportionnalité reliant la température d'un système à son énergie thermique. En effet, la température d'un objet, a priori sensation de chaud ou de froid, se voit définie plus précisément : le kelvin noté K permet une mesure quantitative de la température. Au cours du XIX^e siècle, les physiciens prennent conscience que la sensation de chaud ou de froid est en fait un transfert d'énergie d'un corps vers un autre, sous forme de chaleur. La perception de la température n'est donc rien d'autre que la manifestation d'un transfert d'énergie, l'énergie thermique via une constante de proportionnalité qui se trouve être k :

• E = 1/2 kT (C'est l'expression de l'énergie dans les cas les plus simples avec un seul degré de liberté ;
• plus généralement : E = f/2 kT, où f est le nombre de termes quadratiques dans le hamiltonien, égal à 3 dans un espace à trois dimensions pour une particule libre.).

Il est faux de dire que f est le nombre de degrés de liberté. Si on prend une particule libre sur un axe : le nombre de degré de liberté est égale à 1. En revanche, si cette particule est soumise à une force de rappel (du type ressort): le nombre de degrés de liberté reste égal à 1, mais un second terme quadratique apparaît ! Dans ce nouveau cas, l'énergie devient : E = kT.

Cette constante est donc utilisée dans toute la physique faisant intervenir une température non nulle. On l'utilise pour convertir une grandeur mesurable : la température en kelvin, en une énergie. Elle est un langage commun à tous les phénomènes physiques et intervient donc par exemple dans :

• le calcul du spectre électromagnétique du corps noir ;
• les systèmes suivant une statistique de Maxwell-Boltzmann (ou loi de distribution des vitesses de Maxwell), notamment la loi d'Arrhenius ;
• la constante de Stefan-Boltzmann ;
• la constante de radiation ;
• l'énergie interne d'un gaz parfait.

Valeur

Dans les unités SI, le Comité de données pour la science et la technologie (CODATA) de 2006 recommande la valeur suivante :

Avec une incertitude standard de :

Soit une incertitude relative de :

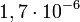
Valeur en Hz/K

Avec une incertitude standard de :

Valeur en eV/K

Avec une incertitude standard de :

Mesure de la constante de Boltzmann (métrologie)

La température absolue (unité le Kelvin) fait partie des 7 unités fondamentales du système international d'unités (SI)

Dans le cadre de la révision du SI en 2011, il sera procédé à une réévaluation de toutes les constantes de Comité de données pour la science et la technologie (CODATA), donc celle de k = R/N_A.

La mesure de N_A a suivi deux voies :

• la mesure du nombre d'atomes dans un cristal de silicium le plus pur possible (réalisé, mais le prix est très onéreux et peu d'États pourraient payer un tel étalon secondaire) ;
• les balances du watt donnent maintenant des résultats performants et concordants en exactitude (c'est-à-dire, que l'on craint moins les erreurs systématiques, car les barres d'erreur se recouvrent).

Néanmoins à terme, il est possible que le nombre d'Avogadro soit défini a priori (ce qui compte, c'est le rapport des masses des atomes. Or les atomes piégeables dans les Penning traps donnent leur masse à 10^-10 près).

La dernière mesure de R (constante des gaz parfaits) est assez ancienne : 1988 au National Institute of Standards and Technology (NIST). On cherche donc à l'améliorer.

• la mesure de la vitesse du son dans un gaz (Moldover), situé dans un résonateur sphérique rempli d'argon, étudiée en fonction de la pression (corrections du viriel) est un exploit technologique assez délicat (variation du volume avec la pression, absorption, désorption). Laurent Pitre opère avec de l'hélium.

• la mesure relative d'une capacité à gaz comparée à celle à vide permet de mesurer la constante diélectrique du gaz et de remonter via la relation de Clausius-Mossotti à kT : la précision est 30 ppm avec l'objectif d'atteindre 1 ppm.

• la mesure du bruit de résistance thermique (relation de Nyquist) ne permettra sans doute pas d'atteindre mieux que 20 ppm, en raison de la bande passante.

• la mesure du rayonnement du corps noir, via la loi de Stefan est limitée à cause de la précision sur l'ouverture (il faut la luminance et non la puissance. Le stéradian intervient) : 30 ppm.

On peut comme en astronomie, définir la température de couleur, mais là c'est l'étalonnage du filtre de bande passante qui est limitant : 100 ppm.

• la mesure de largeur Doppler d'une raie spectrale paraît finalement la meilleure solution : le thermomètre mesure donc la température en hertz. La cuve actuelle du LNE-LNM (Paris XIII) de 250 litres d'un mélange eau-glace à 273,150(3)K contient l'ampoule de gaz ammoniac NH₃ dont on étudie une raie IR caractéristique bien cataloguée, de forte absorption (pour obtenir le meilleur rapport signal sur bruit et pour travailler à plus basse pression). Une nouvelle cuve récemment entrée en service permet de tester l'exactitude : avec un spectre en 38 s et environ 500 en 5 h, on atteint les 50 ppm d'incertitude (Daussy, PRL2007).

Mais se posent encore des problèmes non résolus : le tirage par échantillons n'est pas vraiment homogène (erreurs systèmatiques): il convient donc de repérer les défauts d'exactitude : alignement optique, rétroaction cuve-banc d'optique, modulation de l'intensité du laser CO₂ (en fréquence et en puissance) et de sa chaîne de balayage.

L'avantage de cette méthode est de pouvoir changer de nombreux paramètres (afin de tester expérimentalement l'exactitude), en particulier changer de gaz, CH₄ ou SiCl₄, etc.

On pourra alors balayer un intervalle de température assez conséquent, ce qui améliorera considérablement l'EIT 90 (Échelle internationale de température 1990).

Il est possible qu'à terme, on s'aperçoive que d'autres transitions de phase soient meilleures, puis si on prend l'habitude de mesurer les températures en hertz, c'est-à-dire en joule, via la donnée imposée de la constante de Planck, (soit en eV, si on a la charge de l'électron avec assez de précision), alors on aura réalisé un thermomètre gradué directement en Hz et eV : la boucle se refermera car beaucoup de physiciens des basses températures utilisent déjà cette unité. Or k n'est jamais que le facteur de conversion J/K .

Ce type de situation a déjà été vécu : il fut un temps où l'unité de chaleur était la calorie et l'unité de travail le joule et la calorie/joule s'appelait J et était tabulée par CODATA : J ~ 4.1855 cal/joule. Ensuite on a décidé de prendre la même unité pour la chaleur et le travail, compte-tenu du premier principe de la thermodynamique et de l'expérience de Joule (1845).

Alors la constante de Boltzmann se « fossilisera ». L'entropie se mesurera en bits ou en octets et sera ce qu'elle est réellement : une grandeur sans dimension (mais avec des unités puisqu'il s'agit de z → Ln z : unités le néper et le radian)