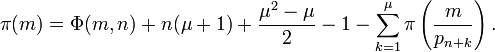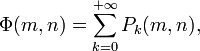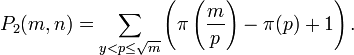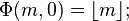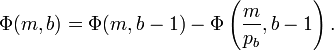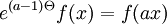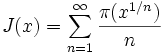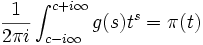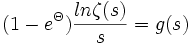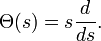Fonction de compte des nombres premiers - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
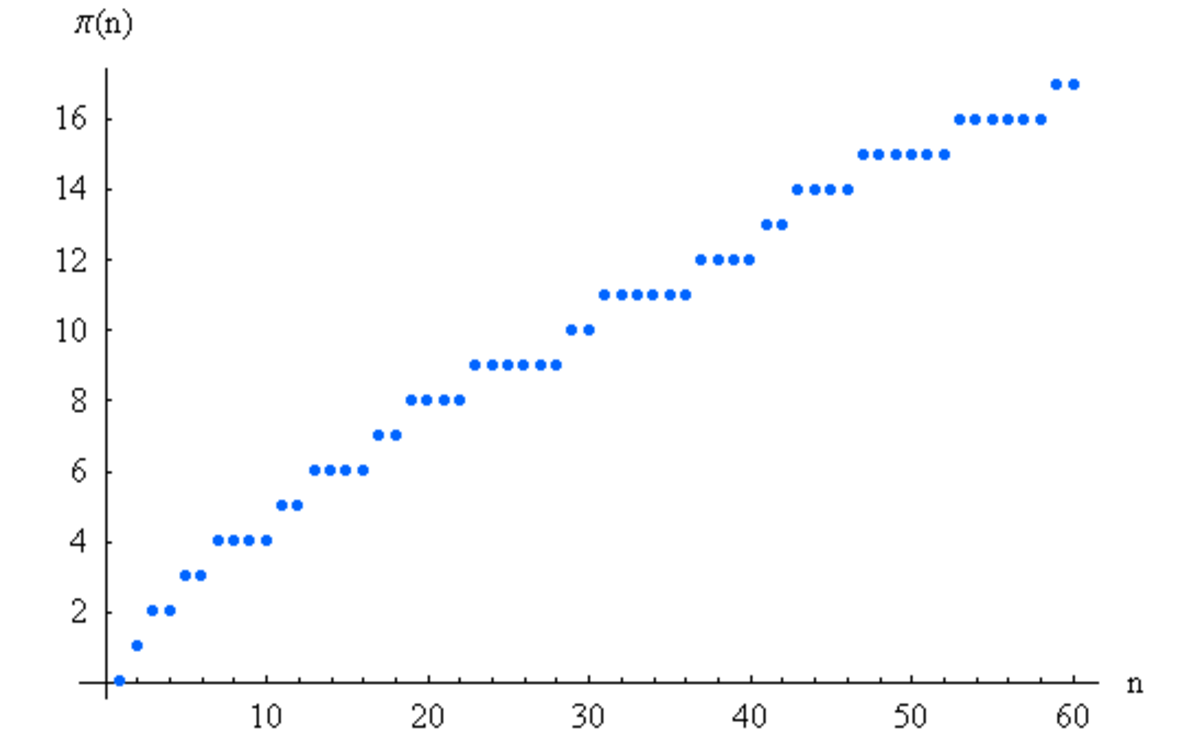
En mathématiques, la fonction de compte des nombres premiers est la fonction comptant le nombre de nombres premiers inférieurs ou égaux à un nombre réel x. Elle est notée
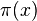
Historique
Depuis Euclide, il est connu qu'il existe des nombres premiers en quantité infinie. Pour affiner la connaissance de ces nombres, la théorie des nombres s'est attelée à en déterminer le taux de croissance. À la fin du XVIIIe siècle, Gauss et Legendre ont conjecturé que cette quantité était proche de
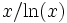
De manière équivalente, on peut l'écrire
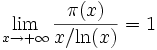
|
Cette affirmation constitue le théorème des nombres premiers, prouvé indépendamment par Hadamard et de La Vallée Poussin, en 1896, grâce à la fonction zêta de Riemann. Une assertion équivalente est:
-
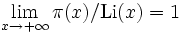
où
Des estimateurs plus précis de
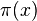
-
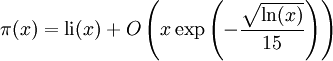
Des preuves du théorème des nombres premiers n'utilisant pas l'analyse complexe furent proposée en 1948 par Atle Selberg et Paul Erdős.
Autres fonctions de compte des nombres premiers
D'autres fonctions de compte des nombres premiers sont aussi utilisées car elles sont plus pratiques pour travailler. Une d'elles est la fonction de compte des nombres premiers de Riemann, notée
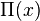
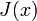
où p est un nombre premier.
Nous pouvons aussi écrire
-
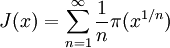
et en connaissant la relation entre la fonction log de la fonction Riemann et la fonction de von Mangoldt
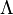
excepté où se trouvent les discontinuités aux puissances de nombres premiers, et ainsi,
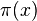
La fonction de Tchebychev pèse les nombres premiers ou les puissances de nombres premiers pn par ln p:
Excepté aux discontinuités des puissances de nombres premiers, nous avons
où
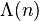
Algorithmes d'évaluation de π(x)
Une façon simple de calculer
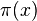


Une manière plus élaborée pour trouver
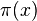

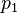
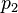
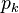
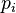
-
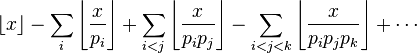

Ce nombre est donc égal à :
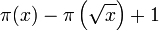
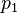
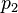
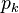

Dans une série d'articles publiés entre 1870 et 1885, Ernst Meissel décrivit (et utilisa) une manière combinatoire pratique pour évaluer
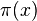
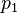
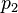
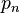
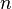
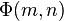
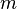
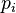
Soit un nombre naturel donné
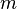
![n=\pi\left(\sqrt[3]{m}\right)\,](https://static.techno-science.net/illustration/Definitions/autres/d/d1ff8835df047e0a61a9c57f3b6bb88e_619f98713a468f6e4a44ae02c1e459a2.png)
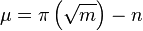
En utilisant cette approche, Meissel calcula
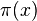

En 1959, Derrick Lehmer étendit et simplifia la méthode de Meissel. Définissons, pour un réel m et pour des nombres naturels n, et k, Pk(m,n) comme le nombre de nombres inférieurs à m avec exactement k facteurs premiers, tous plus grands que pn. De plus, fixons
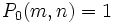
où la somme actuelle possède seulement de manière finie plusieurs termes différents de zéro. Soit y désignant un entier tel que
![\sqrt[3]{m}\le y\le\sqrt{m}\,](https://static.techno-science.net/illustration/Definitions/autres/9/9b72772fdd5ee03360226d6066b332ff_fc181731b98ba45887bb7be7b73e8567.png)
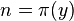
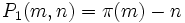
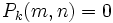
-
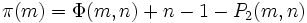
Le calcul de
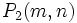
D'un autre côté, le calcul de Φ(m,n) peut être fait en utilisant les règles suivantes :
En utilisant cette méthode et un IBM 701, Lehmer a été capable de calculer
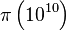
Le mathématicien chinois Hwang Cheng, dans une conférence sur les fonctions de nombres premiers à l'université de Bordeaux utilisa les identités suivantes :
et en notant
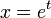
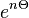
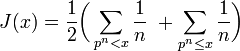
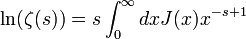
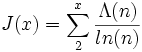
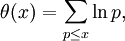
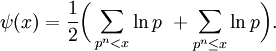
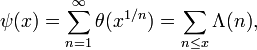
![\Phi(m,n)=\Phi(m,n-1)-\Phi\left(\left[\frac{m}{p_n}\right],n-1\right),\,](https://static.techno-science.net/illustration/Definitions/autres/7/74e174d3340797349db089ff76162460_ae0821b1dca997b6b5f687bc29d8b1ec.png)