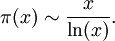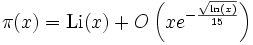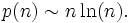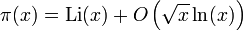Théorème des nombres premiers - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des nombres, le théorème des nombres premiers est un résultat concernant la densité asymptotique des nombres premiers. En définissant, pour tout réel positif x, le nombre π(x) comme le nombre de nombres premiers inférieurs à x, le théorème des nombres premiers s'énonce de la façon suivante :
Théorème des nombres premiers — Lorsque
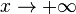
(ln (x) désigne le logarithme naturel de x ; pour la signification de
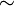
Une meilleure approximation, avec une estimation de l'erreur, est donnée par la formule :
pour de grandes valeurs de x (Li est la fonction logarithme intégral).
Le tableau suivant illustre les écarts entre π(x) et ses approximations, π(x) et Li(x) :
| x | π(x) | π(x) - x / ln(x) | Li(x) - π(x) | x / π(x) |
|---|---|---|---|---|
| 101 | 4 | 0 | 2 | 2,500 |
| 102 | 25 | 3 | 5 | 4,000 |
| 103 | 168 | 23 | 10 | 5,952 |
| 104 | 1 229 | 143 | 17 | 8,137 |
| 105 | 9 592 | 906 | 38 | 10,430 |
| 106 | 78 498 | 6 116 | 130 | 12,740 |
| 107 | 664 579 | 44 159 | 339 | 15,050 |
| 108 | 5 761 455 | 332 774 | 754 | 17,360 |
| 109 | 50 847 534 | 2 592 592 | 1 701 | 19,670 |
| 1010 | 455 052 511 | 20 758 029 | 3 104 | 21,980 |
| 1011 | 4 118 054 813 | 169 923 159 | 11 588 | 24,280 |
| 1012 | 37 607 912 018 | 1 416 705 193 | 38 263 | 26,590 |
| 1013 | 346 065 536 839 | 11 992 858 452 | 108 971 | 28,900 |
| 1014 | 3 204 941 750 802 | 102 838 308 636 | 314 890 | 31,200 |
| 1015 | 29 844 570 422 669 | 891 604 962 452 | 1 052 619 | 33,510 |
| 1016 | 279 238 341 033 925 | 7 804 289 844 392 | 3 214 632 | 35,810 |
| 4 ·1016 | 1 075 292 778 753 150 | 28 929 900 579 949 | 5 538 861 | 37,200 |
Le théorème des nombres premiers permet d'obtenir une formule qui donne le comportement asymptotique du nième nombre premier p(n) :
Histoire
Le théorème des nombres premiers a été conjecturé par Gauss en 1792 alors qu'il avait seulement 15 ans et par Adrien-Marie Legendre en 1798, puis démontré indépendamment par Jacques Hadamard et de la Vallée Poussin en 1896 à l'aide de méthodes d'analyse complexe, en particulier la fonction ζ de Riemann.
À cause de la relation entre la fonction ζ de Riemann et π(x), l'hypothèse de Riemann a une importance considérable en théorie des nombres : si elle était démontrée, cela produirait de loin une bien meilleure estimation de l'erreur intervenant dans le théorème des nombres premiers.
Helge von Koch en 1901 a montré plus précisément, que si l'hypothèse de Riemann était vraie, le terme d'erreur dans la relation mentionnée ci-dessus pourrait être amélioré en :
La constante sous la notation grand O est inconnue.
On est encore loin d'un tel terme d'erreur. En revanche, on sait que toute amélioration de la région sans zéro de la fonction ζ de Riemann améliore de facto le terme d'erreur du théorème des nombres premiers. La meilleure région sans zéro actuellement connue a été obtenue en 1958 par Korobov et Vinogradov [Cette région était un peu trop "optimiste", et n'a jamais été rigoureusement établie, ni par Vinogradov, ni par Korobov, ni par personne d'autre. Elle a été finalement remplacée par une région plus petite (mais établie par une preuve) par H.-E. Richert en 1967]. La région de Richert implique le résultat suivant : lorsque
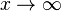
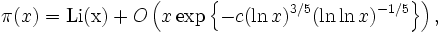
où c > 0 est une constante absolue.
En ce qui concerne des majorations explicites, mentionnons les travaux de Rosser et Schoenfeld (1962, 1975, 1976), puis ceux de Dusart (1998). À l'aide d'ordinateurs de plus en plus puissants, ces chercheurs ont pu déterminer de plus en plus de zéros non triviaux de la fonction ζ sur la droite critique. Cette connaissance de plus en plus approfondie implique de bonnes estimations des fonctions usuelles de nombres premiers, avec ou sans l'hypothèse de Riemann. Ainsi, en 1976, Schoenfeld a-t-il pu établir que, si l'hypothèse de Riemann est vraie, alors on a, pour tout réel
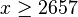
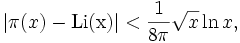
alors que, sans condition, Dusart a démontré que, pour tout réel
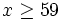
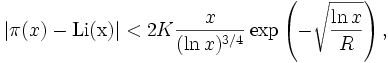
où
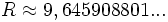
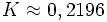
Pour une autre classe des sommes le théorème des nombres premiers peut être généralisé (Weyl)
| ∑ | (pk)˜Li(xk + 1) |
| p |
où Li(x) la fonction intégrale est logarithmique et k>0