Forcing - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Motivations intuitives - Modèles transitifs dénombrables et fitres génériques - Ensembles de conditions de forcing - Le forcing de Cohen - Forcing - Le forcing de Easton - La condition de chaîne dénombrable - Modèles à valeurs booléennes - Réels aléatoires - Une interprétation métamathématique

Forcing

Étant donné un filtre générique G⊆P, la construction du nouveau modèle par forcing est la suivante. La sous-classe des P-noms dans M est notée M^(P). Soit M[G]={val(u,G):u∈M^(P)}. Pour ramener l'étude de la théorie des ensembles de M[G] à celle de M, on travaille dans le langage du forcing, qui est celui du calcul des prédicats du premier ordre avec l'appartenance comme relation binaire et tous les noms comme constantes.

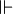
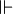
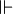
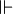
Définissons alors p $\Vdash$ φ(u₁,…,u_n) (qui se lit "p force φ") où p est une condition, φ est une formule du langage du forcing, et les u_i sont des noms, comme signifiant que si G est un filtre générique contenant p, alors M[G] ⊨ φ(val(u₁,G),…,val(u_n,G)). Le cas particulier 1 $\Vdash$ φ est souvent noté P $\Vdash$ φ ou $\Vdash$ φ. Ces assertions sont vraies dans M[G] quel que soit le choix de G.

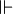
L'important est que cette définition "externe" de la relation de forcing p $\Vdash$ φ est équivalente à une définition "interne", par récurrence transfinie sur les noms pour les occurrences de u ∈ v et de u = v, suivie d'une récurrence ordinaire sur la complexité des formules. Cela a pour conséquence que toutes les propriétés de M[G] sont en fait des propriétés de M, et la vérification dans M[G] des axiomes de ZFC en devient élémentaire. On résume généralement cela par les trois propriétés suivantes :

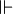
Vérité : M[G] ⊨ φ(val(u₁,G),…,val(u_n,G)) si et seulement si pour une certaine condition p ∈ G, p $\Vdash$ φ(u₁,…,u_n) (la formule φ est forcée par G).
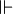
Définissabilité : L'assertion "p $\Vdash$ φ(u₁,…,u_n)" est définissable dans M.
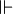
Cohérence : si p $\Vdash$ φ(u₁,…,u_n) et q ≤ p, alors q $\Vdash$ φ(u₁,…,u_n).

On peut résumer ce qui précède en disant que le résultat fondamental de cohérence est qu'étant donné un ensemble de conditions P, on peut supposer qu'il existe un filtre générique G, non dans l'univers V, tel que V[G] est encore un univers, donc un modèle de ZFC. De plus, les assertions vraies dans V[G] se ramènent à des assertions vraies dans V par rapport à la relation de forcing.

Les deux styles, soit l'adjonction de G à un modèle transitif dénombrable M , soit à l'univers entier V, sont fréquemment employés. On rencontre moins souvent l'approche utilisant la définition "interne" du forcing, sans mentionner de modèles. Cette dernière méthode est celle qu'avait utilisée Cohen initialement, et qui est devenue la méthode de l'analyse des valeurs booléennes.

Le forcing de Easton

La valeur exacte de 2^ℵ₀ dans le modèle de Cohen, ainsi que dans des variantes telles que Fin(ω × κ , 2) pour des cardinaux κ quelconques, fut déterminée par Robert M. Solovay, qui montra également comment construire des modèles où l'hypothèse du continu généralisée est fausse pour un nombre fini de cardinaux réguliers. Ainsi, dans le modèle de Cohen, si 2^ℵ₀ = ℵ₁ est vrai dans V, alors 2^ℵ₀ = ℵ₂ est vrai dans V[G].

En 1970, W. B. Easton montra comment violer l'hypothèse du continu généralisée pour un nombre infini, et même une classe propre, de cardinaux réguliers, démontrant que les restrictions connues sur les valeurs des puissances des cardinaux réguliers (monotonie, théorème de Cantor et théorème de König) étaient les seules prouvables dans ZFC.

Ce travail introduisit l'idée du forcing avec une classe propre de conditions. En général, cette technique échoue à construire un modèle de ZFC. Par exemple, Fin (ω × On , 2), où "On" est la classe de tous les ordinaux, fait du continu une classe propre. Fin (ω , On) permet une énumération (dénombrable) des ordinaux. Dans les deux cas, le V[G] qui en résulte n'est clairement pas un modèle de ZFC.

À cette époque, on pensait que des méthodes de forcing plus sophistiquées permettraient de même de construire des valeurs arbitraires des puissances des cardinaux singuliers. Mais le problème s'est avéré difficile, avec l'apparition de nouvelles restrictions démontrables dans ZFC, et les modèles obtenus par forcing dépendant parfois de divers axiomes de grands cardinaux ; il reste encore de nombreuses questions ouvertes.