Forcing - Définition

Ensembles de conditions de forcing

Un ensemble partiellement ordonné de conditions de forcing, abrégé ici en ensemble de conditions, est un triplet (P, ≤, 1), où "≤" est un pré-ordre sur P, et où 1 est un élément maximal, c'est-à-dire que p ≤ 1 pour tous les p de P. Les éléments de P sont appelés des conditions. On lit p ≤ q comme "p est plus forte que q" (ou encore "p raffine q").

Intuitivement, les conditions "plus petites" fournissent davantage d'informations, tout comme l'intervalle plus étroit [3.1415926,3.1415927] fournit davantage d'informations sur le nombre π que ne le fait l'intervalle [3.1,3.2].

Associés à un ensemble de conditions donné P, on définit les P-noms, qui sont les ensembles de la forme {(u,p):u est un P-nom et p P}. Cette définition est circulaire, ce qui, dans ce contexte, veut dire qu'il s'agit en réalité d'une définition par récurrence transfinie ; une formulation rigoureuse consisterait par exemple à définir :

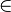
• Nom(0) = {};
• Nom(α + 1) = l'ensemble des sous-ensembles de (Nom(α) × P);
• Nom(λ) = {Nom(α) : α < λ}, si λ est un ordinal limite,

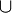
et alors la classe des P-noms est définie comme étant

V^(P) = {Nom(α) : α est un ordinal}.

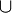
Les P-noms constituent une extension de l'univers : étant donné x dans V, on définit xˇ comme étant le P-nom {(yˇ,1) : y x}. Là encore, il s'agit en fait d'une définition par récurrence transfinie.

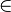
Ėtant donné un sous-ensemble quelconque G de P, on définit ensuite, toujours par récurrence transfinie, l'application d'interprétation (ou de valuation) sur les noms par val(u, G) = {val(v, G) : ∃ p ∈ G , (v, p) ∈ u}. Remarquons que si 1 est dans G, alors val(xˇ, G) = x. On définit enfin G = {(pˇ, p) : p ∈ G}, et alors val(G,G) = G.

Un bon exemple d'ensemble de conditions de forcing est (Bor(I) , ⊆ , I ), où I = [0,1] et Bor(I) sont les sous-ensembles boréliens de I de mesure de Lebesgue non nulle. Dans ce cas, on peut interpréter les conditions comme étant des probabilités, et un Bor(I)-nom définit l'appartenance en un sens probabiliste. Cet exemple permettant une visualisation assez intuitive, le langage des probabilités est parfois utilisé également avec d'autres ensembles de conditions de forcing.

Le forcing de Cohen

L'ensemble de conditions (non trivial) le plus simple est ( Fin(ω,2) , ⊇ , 0 ), l'ensemble des fonctions définies sur une partie finie de ω à valeur dans 2={0,1}, ordonné par l'inclusion inverse, c'est-à-dire qu'une condition p peut être vue comme formée de deux sous-ensembles finis disjoints de ω, p⁻¹[1] et p⁻¹[0], que l'on peut voir comme les parties "oui" et "non" de p, aucune information n'étant donnée sur le complémentaire de ces sous-ensembles. Dire que q est plus forte que p signifie que q ⊇ p, autrement dit que les parties "oui" et "non" de q contiennent celles de p, donc donnent à ce sens davantage d'informations.

Soit G un filtre générique pour cet ensemble de conditions. Si p et q appartiennent à G, p∪q est également une condition, puisque G est un filtre. Cela veut dire que g=⋃G est fonctionnelle, car deux conditions de G ont les même valeurs sur l'intersection de leurs domaines.

g est en fait une fonction partout définie sur ω : étant donné n ∈ ω, soit D_n={ p : p(n) est défini }, alors D_n est dense (car pour un p tel que n ne soit pas dans le domaine de p, en adjoignant une valeur quelconque pour n, le résultat sera dans D_n). Une condition p ∈ G∩D_n a n dans son domaine, et comme p ⊆ g, g(n) est défini.

Soit X=g⁻¹[1], l'ensemble des réponses "oui" des conditions génériques. On peut déterminer un nom pour X directement. Soit X = { ( nˇ , p ) : p(n)=1 } ; on a donc val( X , G ) = X. Supposons alors que A⊆ω soit dans V. Nous allons montrer que X≠A. Soit D_A = { p : ∃n, n∈dom(p) et p(n)=1 si et seulement si n∉A }. D_A est dense (en effet, étant donné p, si n n'est pas dans le domaine de p, il suffit d'adjoindre pour n une valeur opposée à celle de "n∈A"). Ainsi, tout p∈G∩D_A force X≠A. En résumé, X est un nouveau sous-ensemble de ω, nécessairement infini.

La même construction, où ω est remplacé par ω×ω₂, c'est-à-dire qu'on considère des fonctions définies sur un sous-ensemble fini de couples de la forme (n,α), avec n<ω et α<ω₂, et ayant pour valeurs 0 ou 1, aboutit à créer ω₂ nouveaux sous-ensembles de ω. Ces sous-ensembles sont tous distincts, par un argument de densité : étant donné α<β<ω₂, soit D_α,β={p:∃n, p(n,α)≠p(n,β)} ; alors chaque D_α,β est dense, et une condition générique dans cet ensemble prouve qu'il y a un entier qui distingue le α-ème nouvel ensemble du β-ème, c'est-à dire qu'il appartient à l'un des deux, mais pas à l'autre.

Ceci ne suffit pas à falsifier l'hypothèse du continu, car il faut encore montrer qu'on n'a pas créé de nouvelles applications qui seraient des bijections entre ω et ω₁, ou entre ω₁ et ω₂. Ainsi, si l'on avait pris comme ensemble de conditions Fin(ω,ω₁) (les applications allant des parties finies de ω vers ω₁), on aurait dans V[G] une bijection de ω vers ω₁, et donc ω₁ serait devenu un ordinal dénombrable dans V[G] (on dit dans ce cas que ω₁ s'est effondré).

C'est pourquoi la dernière étape dans la démonstration de l'indépendance de l'hypothèse du continu est de montrer que le forcing de Cohen n'effondre pas les cardinaux. Cette démonstration utilise une propriété combinatoire pour montrer que toutes les antichaînes de cet ensemble de conditions sont dénombrables, comme on le verra dans la section suivante.