Forcing - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus précisément en logique mathématique, le forcing est une technique inventée par Paul Cohen pour prouver des résultats de cohérence et d'indépendance en théorie des ensembles. Elle a été utilisée pour la première fois en 1962 pour prouver l'indépendance de l'hypothèse du continu vis-à-vis de la théorie ZFC. Combinée avec la technique des modèles de permutation de Fraenkel-Mostowski-Specker, elle a permis également d'établir l'indépendance de l'axiome du choix relativement à ZF. Le forcing a été notablement remanié et simplifié dans les années soixante et s'est révélé être une technique extrêmement puissante, à la fois en théorie des ensembles et dans d'autres branches de la logique mathématique, comme la théorie des modèles ou la logique intuitionniste.
Motivations intuitives
Le forcing est équivalent à la méthode des modèles à valeurs booléennes, qui est parfois ressentie comme plus naturelle et intuitive, mais qui est en général plus difficile à appliquer.
Intuitivement, le forcing consiste à étendre l'univers V. Dans cet univers plus large, V*, on pourra par exemple avoir de nombreux nouveaux sous-ensembles de ω = {0,1,2,…} qui n'existaient pas dans l'univers V, violant ainsi l'hypothèse du continu. A priori impossible, cette construction ne fait que refléter l'un des "paradoxes" de Cantor concernant l'infini, et en particulier le fait qu'il existe des modèles dénombrables de ZFC, contenant pourtant des ensembles non-dénombrables (au sens du modèle), d'après le théorème de Löwenheim-Skolem. En principe, on pourrait par exemple considérer
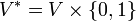
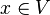
La technique initialement définie par Cohen, connue à présent sous le nom de forcing ramifié, est légèrement différente du forcing non ramifié qui sera exposé ici.
Modèles transitifs dénombrables et fitres génériques
L'étape clé de la technique du forcing est, étant donné un univers V de ZFC, de déterminer un G approprié qui ne soit pas dans V. La classe de toutes les interprétations des P-noms s'avèrera être un modèle de ZFC, et une extension propre du V initial, puisque G∉V.
Plutôt que de travailler avec V, on considère un modèle transitif dénombrable M, avec (P,≤,1) ∈ M. M est ici un modèle de la théorie des ensembles, soit de tout ZFC, soit d'un sous-ensemble fini des axiomes de ZFC, ou encore d'une variante. La transitivité signifie que si x ∈ y ∈ M, alors x ∈ M ; le lemme de Mostowski dit qu'on peut supposer la transitivité de M si la relation d'appartenance est bien fondée. La transitivité permet de traiter l'appartenance et les autres propriétés élémentaires des ensembles de manière intuitive dans M. Enfin, il est toujours possible de prendre des modèles dénombrables, grâce au théorème de Löwenheim-Skolem.
M étant un ensemble, il y a des ensembles non dans M (c'est le paradoxe de Russell). L'ensemble G approprié, qu'on choisit d'adjoindre à M, doit être un filtre générique sur P, c'est-à-dire un sous-ensemble de P tel que
-
- 1 ∈ G ;
- si p ≥ q ∈ G, alors p ∈ G ;
- si p,q ∈ G, alors ∃r ∈ G, r ≤ p et r ≤ q ;
ce qui fait de G un filtre ; la condition pour que G soit générique est
-
- si D ∈ M est un sous-ensemble dense de P (c'est-à-dire, si p ∈ P implique ∃q ∈ D, q ≤ p) alors G∩D ≠ 0 .
L'existence d'un filtre générique G non dans M découle du lemme de Rasiowa-Sikorski. En fait, on a un résultat légèrement plus fort : étant donnée une condition p ∈ P, il existe un filtre générique G tel que p ∈ G.
Si P n'a qu'un ensemble dénombrable de sous-ensembles denses, on peut en fait choisir G ∈ M ; c'est le cas trivial. Les éléments minimaux de P donnent aussi des G triviaux ; en effet si D est dense et si p est minimal, alors, comme le seul element q ≤ p est p lui-même, p ∈ D. Ainsi, tout filtre contenant un élément minimal est générique, et l'on peut encore choisir G ∈ M.

















































