Fractale du mot de Fibonacci - Définition

Références et bibliographie

Tuile de Fibonacci

Pavage (imparfait) par des tuiles de Fibonacci. L'espace non couvert tend vers zéro à l'infini

Pavage parfait par des flocons de Fibonacci

La juxtaposition de 4 courbes de Fibonacci de type F_3k permet la construction d'une courbe fermée délimitant une surface connexe d'aire non nulle. Cette figure est appelée "tuile de Fibonacci".

• La tuile de Fibonacci pave presque le plan. Elle laisse un carré libre dont la surface tend vers zéro à mesure que k tend vers l'infini. A la limite, la tuile de Fibonacci pave le plan.
• Si la tuile de Fibonacci s'inscrit dans un carré de côté 1, alors son aire tend vers .

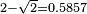
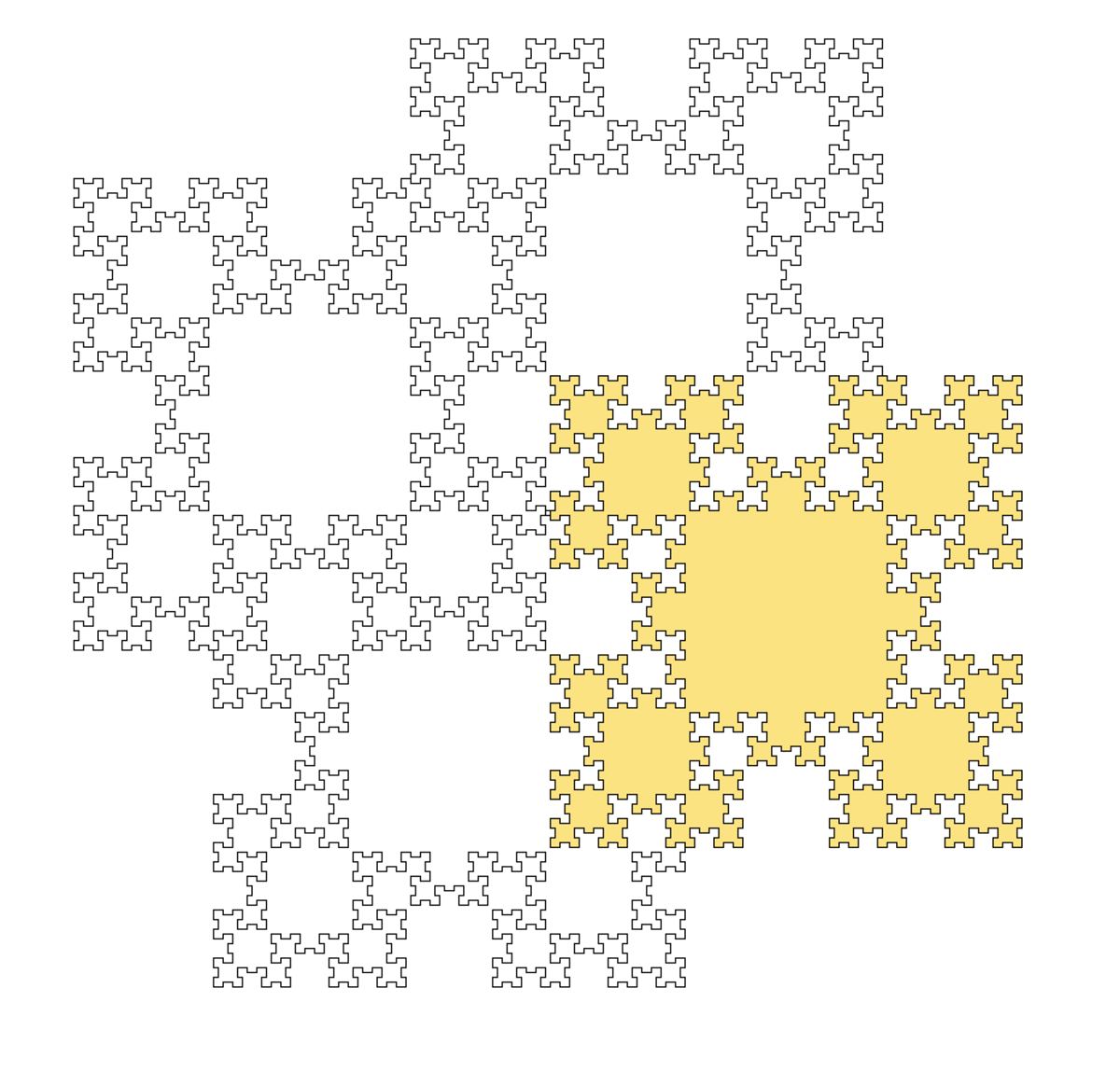
Flocon de Fibonacci

Le flocon de Fibonacci est une tuile de Fibonacci définie selon la règle suivante :

• si
• sinon.

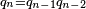
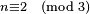
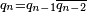
Avec q₀ = ε et q₁ = D, G = "tourne à gauche" et D = "tourne à droite", et ,

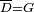
Quelques propriétés remarquables :

• C'est la tuile de Fibonacci associée à la variante "diagonale" définie précédemment.
• Il pave le plan à toute itération (à tout ordre)
• Il pave le plan par translation de deux façons différentes, il s'agit donc d'un double pseudo-carré.
• son périmètre, à l'ordre n, vaut 4F(3n + 1). F(n) étant le nième nombre de Fibonacci.
• son aire, à l'ordre n, suit les index successifs de rang impair de la suite de Pell (définie par P(n) = 2P(n − 1) + P(n − 2)).