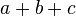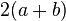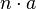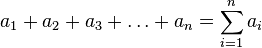Périmètre - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le périmètre d'une figure plane est la longueur du bord de cette figure. Le calcul du périmètre sert par exemple à déterminer la quantité de grillage nécessaire à la clôture d'un terrain, le nombre de briques ou de pierres pour la construction d'un mur, etc.
Pour tout polygone, le périmètre vaut la somme des longueurs des côtés du polygone. Il existe des formules simples pour le calcul du périmètre des figures de base, mais le problème devient beaucoup plus ardu pour des figures plus complexes : il fait appel à des calculs d'intégrales ou de limites. Dans ce cas, une méthode consiste à approcher la figure complexe par d'autres, plus simples et mieux connues, pour obtenir une approximation du périmètre voulu.
La question de savoir, pour un périmètre donné, quelle est la surface dont l'aire est maximale (ou isopérimétrie) a été posée très tôt et sa réponse seulement démontrée au XIXe siècle.
Le périmètre désigne aussi parfois la courbe qui est le bord d'une surface, plutôt que sa mesure. Le mot périmètre (du grec ancien : περίμετρος) est composé du préfixe péri- qui signifie « autour » et du suffixe -mètre : « mesure ».
Figures de base
Polygone
Le cas des polygones est fondamental, non seulement par sa simplicité, mais aussi parce que de nombreux périmètres sont calculés, en valeur approchée, par une suite de polygones tendant vers ces courbes. Le premier mathématicien connu pour avoir utilisé ce raisonnement fut Archimède qui approcha le périmètre d'un cercle en l'encadrant par celui de polygones réguliers.
Le périmètre d'un polygone est égal à la somme des longueurs de ses côtés.
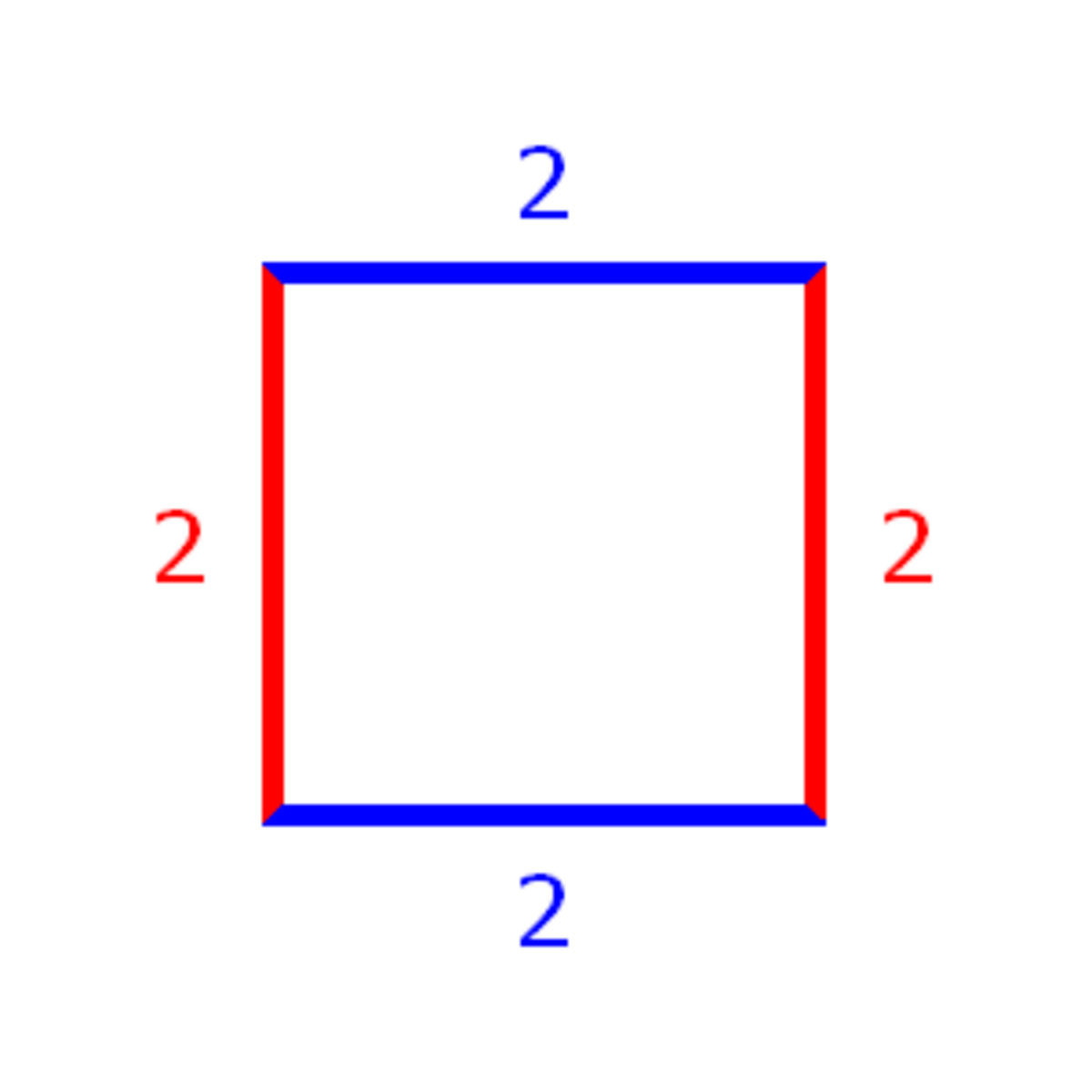
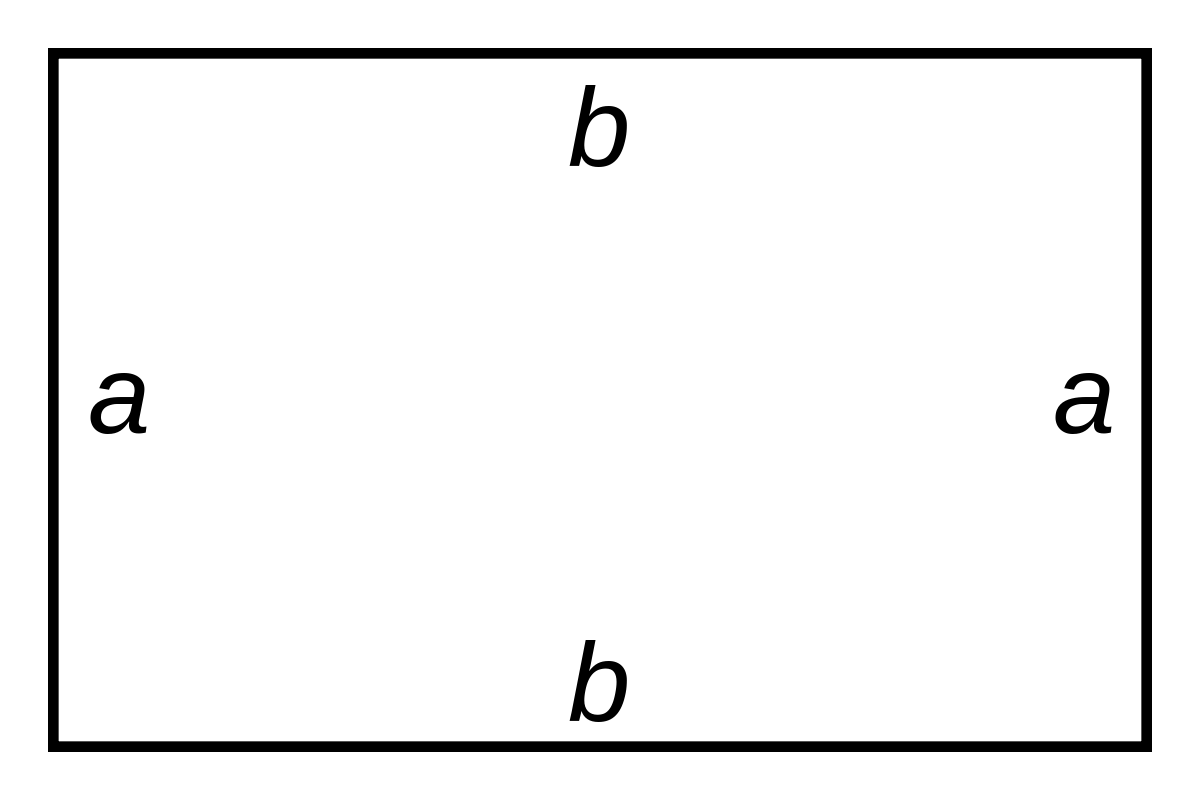
En particulier, un rectangle de dimensions a et b a pour périmètre 2(a + b). Un polygone équilatéral est un polygone dont tous les côtés ont la même longueur (un losange est un polygone équilatéral à quatre côtés). Pour calculer le périmètre d'un polygone équilatéral, il suffit de multiplier cette longueur par le nombre de côtés.
Un polygone régulier est souvent défini par son nombre de côtés et son rayon, c'est-à-dire la distance constante qui sépare son centre de chacun des sommets. Il est possible de calculer la longueur du côté par un raisonnement de trigonométrie. Si R est le rayon d'un polygone régulier et n le nombre de ses côtés, son périmètre est :
-
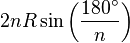
Ces méthodes sont résumées dans le tableau ci-dessous.
| Polygone | Formule | Variables |
|---|---|---|
| Triangle |
| a, b et c sont les longueurs des côtés du triangle. |
| Parallélogramme |
| a et b sont les longueurs de deux côtés consécutifs. |
| Polygone équilatéral |
| n est le nombre de côtés et a la longueur de chaque côté. |
| Polygone quelconque |
| où ai est la longueur du ie (1er, 2e, 3e ... ne) côté d'un polygone à n côtés. |
| Polygone régulier convexe |
| n est le nombre de côtés et R la distance entre le centre du polygone régulier et chacun des sommets. |
Circonférence d'un cercle
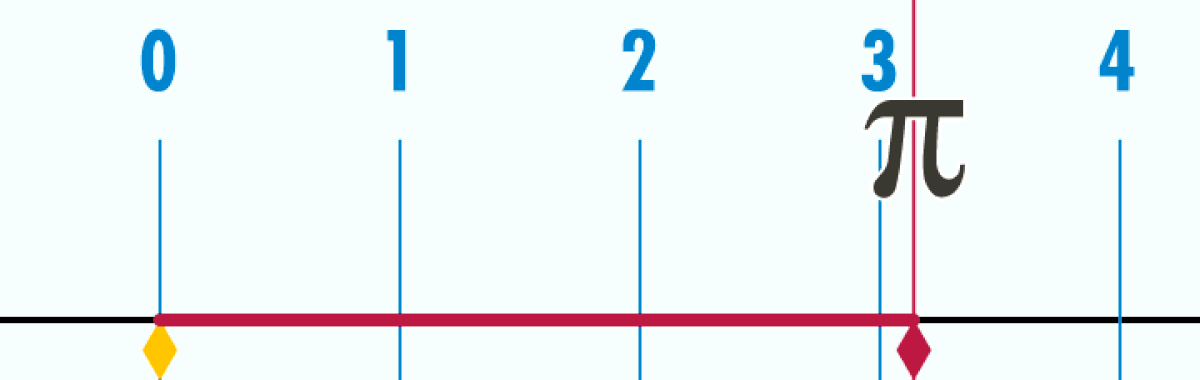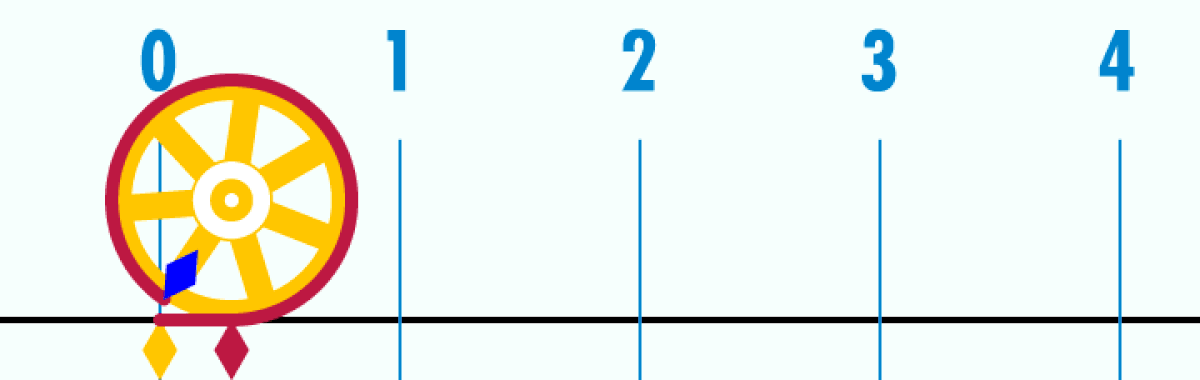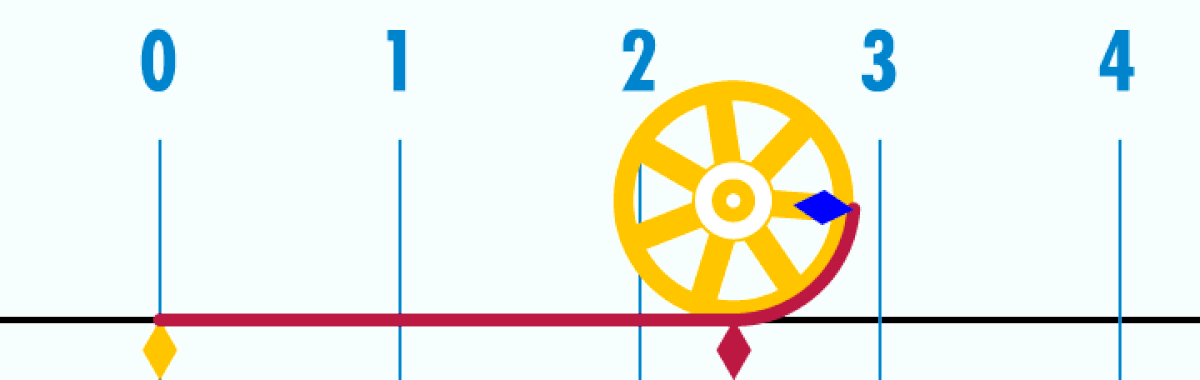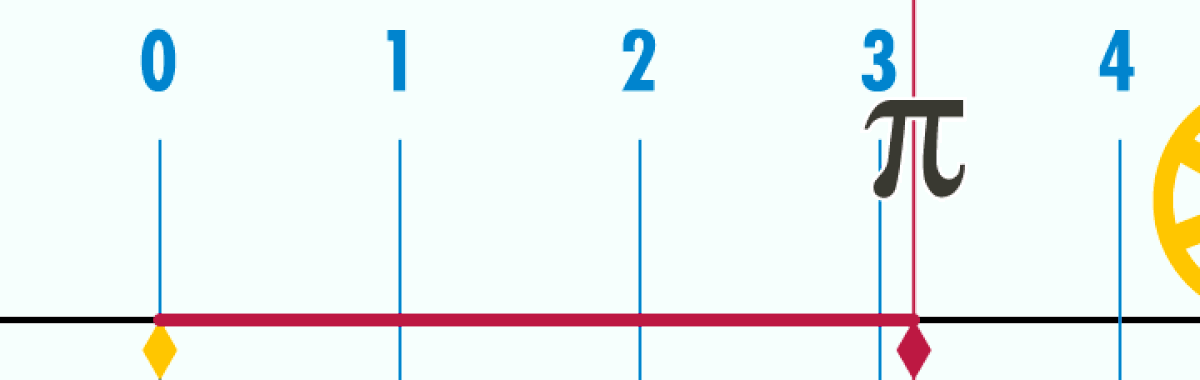
Le périmètre d'un cercle est proportionnel à son diamètre. C'est-à-dire qu'il existe une constante π (le p grec de périmètre) telle que, quel que soit un cercle de diamètre D et de périmètre P,
- P = π D.
L'usage du compas ayant favorisé l'utilisation du rayon R du cercle plutôt que de son diamètre, cette formule devient :
- P = 2 π R.
Ces deux formules sont parfaitement équivalentes puisque, pour tout cercle, D = 2 R.
Il suffit, pour calculer le périmètre d'un cercle, de connaître son rayon ou son diamètre et le nombre π. Le problème est que ce nombre n'est pas rationnel (on ne peut pas l'écrire sous la forme d'un quotient de deux entiers) ni même algébrique (il n'est pas la racine d'un polynôme à coefficients entiers). Obtenir une valeur approchée de π aussi précise qu'on le souhaite n'est donc pas évident. La recherche des décimales de π mobilise des connaissances en analyse, algorithmique et informatique.
Le périmètre d'un cercle est souvent appelé circonférence, parfois longueur, le mot périmètre concernant plutôt le disque.