Homologie singulière - Définition
La liste des auteurs de cet article est disponible ici.
Propriétés
Homologie et connexité par arcs
On montre que H0(X) est le groupe libre commutatif (ou le module libre) ayant autant de générateurs qu'il y a de composantes connexes par arcs de X. En particulier, si X est connexe par arcs, H0 est isomorphe à
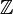
Par ailleurs, si X se décompose en sa famille Xk de composantes connexes par arcs, alors, pour tout q, Hq(X) est égal à la somme directe des Hq(Xk). Il suffit donc de chercher les groupes d'homologie d'espaces connexes par arcs.
Homologie et homotopie
Soit X un espace connexe par arcs. Un 1-cycle de X est une 1-chaîne dont le bord est nul. Intuitivement, on peut le voir comme un chemin qui se referme, ou un lacet. Par ailleurs, un 1-bord est le bord d'une 2-chaîne. Si ce bord se décompose en deux cycles, ces deux cycles seront considérés comme égaux dans le groupe d'homologie H1(X), celui-ci étant le quotient de l'ensemble des cycles par l'ensemble des bords. Par ailleurs, on conçoit qu'on puisse déformer continûment l'un des cycles en l'autre en passant par la surface dont ils constituent les bords. On reconnaît alors la notion d'homotopie. Il n'est donc pas étonnant qu'il existe un rapport entre le premier groupe d'homotopie ou groupe fondamental de Poincaré π1(X) et le premier groupe d'homologie H1. Le théorème d'Hurewicz énonce que l'application qui, à une classe d'homotopie d'un lacet, associe la classe d'homologie de la 1-chaîne correspondant à ce lacet, est un morphisme surjectif de π1(X) sur H1(X), dont le noyau est le sous-groupe des commutateurs de π1(X). Il en résulte que H1(X) est l'abélianisé de π1(X), autrement dit isomorphe à π1(X) après avoir rendu la loi de composition du groupe commutative.
Par exemple, le groupe fondamental d'un espace X en forme de 8 est le groupe libre engendré par deux éléments. Son groupe d'homologie H1 est le groupe abélien libre engendré par deux éléments.
Nombres de Betti et caractéristique d'Euler
Considérons le n-ème groupe d'homologie Hn. Il possède en général un sous-groupe de torsion T, constitué de ses éléments ayant un ordre non nul fini. Le groupe quotient Hn / T est alors un groupe libre dont le nombre bn de générateurs est le rang de Hn, et s'appelle n-ème nombre de Betti.
On définit alors la caractéristique d'Euler de l'espace X comme étant égale à :
| χ(X) = | ∑ | ( − 1)nbn |
| n |
si cette somme a un sens. Dans le cas d'un espace X construit à partir de a0 points, reliés par a1 chemins, liés par a2 faces, etc... on montre que :
| χ(X) = | ∑ | ( − 1)nan |
| n |
Résultats
Le calcul effectif des groupes d'homologie est en général difficile. Nous donnons ici les résultats les plus classiques. Une version simplifiée de l'homologie singulière, l'homologie simpliciale permet de calculer les groupes d'homologie des espaces topologiques admettant une triangulation.
- La sphère Sn de
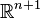
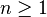
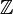
- La boule Bn de
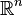
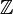
- Le plan projectif :
-
-
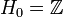
-
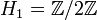
- Hq = 0 si
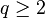
-
Sur cet exemple, on voit que le plan projectif n'est pas homéomorphe au disque du plan, puisqu'ils ne possèdent pas le même H1.
- Plus généralement, l'espace projectif
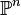
-
-
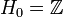
- Hq = 0 si
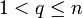
-
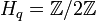
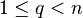
-
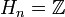
- Hq = 0 si q > n
-
- Le tore
-
-
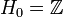
-
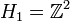
-
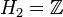
- Hq = 0 si q > 2
-

















































