Homologie singulière - Définition

Introduction

En topologie algébrique, l'homologie singulière est une construction qui permet d'associer à un espace topologique X une suite homologique de groupes abéliens libres ou de modules. Cette association est un invariant topologique, de sorte que deux espaces homéomorphes auront même homologie singulière. Ainsi, pour montrer que deux espaces topologiques ne sont pas homéomorphes, il suffit d'exhiber deux modules différents de leurs suites homologiques.

Le complexe

Avant de définir l'homologie singulière d'un espace topologique X, il est nécessaire d'introduire quelques définitions.

Simplexes

On appelle simplexe standard Δ_n de dimension n l'enveloppe convexe dans des points e₀, e₁, ..., e_n, où e₀ = (0,...,0) et où e_i = (0...,0,1,0,...,0), le 1 étant placé à la i-ème position.

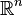
Un simplexe singulier de dimension n de X est une application continue de Δ_n dans X. Ainsi, un 0-simplexe s'identifie à un point de X. Un 1-simplexe est un chemin reliant deux points — éventuellement confondus — paramétré par [0 ; 1]. Un 2-simplexe est un triangle plein de X (ou plutôt une application du triangle Δ₂ dans X).

On considère ensuite les sommes formelles de n-simplexes, c'est-à-dire les fonctions f : {simplexes de dim n de X} → Z à support fini. On les appelle n-chaînes. L'ensemble M_n des n-chaînes constitue un groupe abélien libre, ou un module libre si on se place dans un anneau autre que Z.

L'application bord

Si σ est un simplexe de X de dimension n > 0, la i-ème face σ_i de σ est la restriction de l'application au simplexe standard de dimension n-1, enveloppe convexe des points e₀, ..., e_{i − 1}, e_{i + 1}, ..., e_n.

Le bord de σ est par définition égal à . On convient que le bord d'un point (un 0-simplexe) est 0. L'application bord est étendue par linéarité aux chaînes. On obtient alors un morphisme de M_n dans M_{n − 1} (Si n=0, M _{− 1} = 0) . Le bord d'une chaîne partage des analogies avec la notion de frontière d'une partie, mais cette dernière est une partie de X alors que le bord est un objet purement algébrique, sur lequel on peut effectuer des opérations.

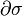
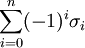
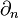
Par exemple, le bord d'un 1-simplexe reliant le point P au point Q est égal à Q - P. Le bord d'un 2-simplexe de sommets P, Q, R est égal à (QR) - (PR) + (PQ), en notant (QR) le chemin reliant Q à R, en se restreignant au premier côté de Δ₂. On remarque que, si on prend le bord de (QR) - (PR) + (PQ), on obtient R - Q - R + P + Q - P = 0.

Plus généralement, on montre que la composition successive de deux applications bord est nulle. Autrement dit, . On dit que la suite des groupes ou modules M_n munie de l'application bord forme un complexe de chaines.

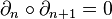
En général le complexe construit est très gros et incalculable en pratique. Par exemple, le premier groupe, d'indice zéro, est le groupe des sommes formelles, à coefficients entiers relatifs, des points de l'espace étudié : c'est un groupe abélien libre de rang le cardinal de X.

Cycles et bords, groupes d'homologies

Puisque , on a . Les éléments de sont appelés bords ; ce sont les chaînes qui sont images d'une autre chaîne par l'application bord. Les éléments de sont appelés cycles ; ce sont les chaînes dont le bord est nul. Tout bord est un cycle.

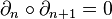
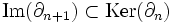
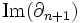
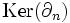
Par exemple, si on convient que le bord d'un point est nul, alors une 0-chaîne s'écrit sous la forme où n est un entier relatif et P un point quelconque de X, la somme étant finie. Toute telle chaîne est un cycle. C'est un bord s'il existe une 1-chaîne dont elle est le bord.

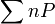
Le groupe quotient ou module quotient est le n-ème groupe H_n d'homologie singulière de l'espace topologique X. C'est un invariant topologique. On associe ainsi à tout espace topologique une suite de groupes abéliens.

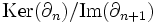
Par exemple (comme toute chaîne de dimension 0) P - Q est un cycle. Il sera considéré comme nul dans H₀ si c'est un bord. Il suffit qu'il soit le bord d'un chemin reliant P à Q. C'est le cas si P et Q sont dans la même composante connexe par arcs de X.