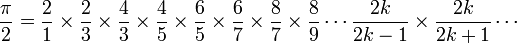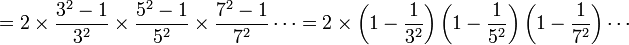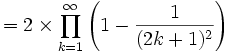John Wallis - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
John Wallis, né le 23 novembre 1616 à Ashford, et mort le 28 octobre 1703 à Oxford, est un mathématicien anglais. Ses travaux sont précurseurs de ceux de Newton. Il est également précurseur de la phonétique, de l'éducation des sourds et de l'orthophonie.
Biographie
Wallis a fait ses études à Cambridge, à l'Emmanuel College d'abord, puis au Queen's college. Étudiant d'abord la théologie, il est ordonné en 1640. Il se réoriente ensuite vers les mathématiques et montre un grand talent pour la cryptographie durant la guerre civile, en décryptant les messages des royalistes. Il occupe ensuite la chaire savilienne de géométrie à l'université d'Oxford, succédant à Peter Turner, renvoyé car royaliste. Il a été l'un des fondateurs de la Royal Society.
Œuvres
- Arithmetica Infinitorum, Oxford, 1655
- Opera, 1670-1671
- Treatise of Algebra, Londres, 1685
- Mathesis Universalis, Oxford, 1685
- De sectionibus conicis
- Operum mathematicorum pars prima, Oxford, 1657
- Tractatus Prœmialis. De loquela, sive Literarum omnium Formatione & genuino Sono, Oxford, Leon Lichfield, 1653. (Traité préliminaire. De la parole ou de la formation de toutes les lettres et du son originel.
- Grammatica Linguae Anglicanae, cui praefigitur de loquela sive de sonorum omnium loquelarum formatione tractatus grammatico physicus, Oxford, Leon Lichfield, 1653. (Grammaire de la langue anglaise, laquelle est précédée d'un traité physico-grammatical sur la parole ou la formation des sons.
- La lettre du Dr John Wallis à Robert Boyle, Philosophical Transactions, 1670.
- La lettre du Dr John Wallis à Mr Thomas Beverly, Philosophical Transactions, 1698.
- Trois rééditions de la seule partie phonétique (1721, Königsberg, 1727 et 1740, Leiden), comportant en annexe le traité de Johann Conrad Amman Surdus loquens, ont aussi été publiées.
Travaux
En mathématiques
Ses travaux concernent principalement le calcul différentiel et intégral où il introduit les intégrales de Wallis d'allure générale :
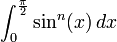
On lui doit également le symbole de l'infini (∞,
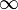
Il assista l'astronome Jeremiah Horrocks pour ses calculs d'éphémérides, notamment lors du transit de Vénus de 1639.
Il résolut le problème de la voûte quarrable (1692), posé par Vincenzo Viviani : trouver une fenêtre dans une voûte hémisphérique de sorte que le reste de la voûte soit quarrable, c'est-à-dire dont l'aire puisse s'écrire c², où c est un nombre constructible à la règle et au compas.
Produit de Wallis
Cette formule a permis à William Brouncker d'obtenir un développement en fraction continue généralisée de 4 / π.
En phonétique et éducation des sourds-muets
Wallis est l'auteur du premier traité de phonétique de la langue anglaise, en introduction à sa Grammatica Linguae Anglicanae. Il est également connu comme précurseur de l’éducation des sourds-muets. Il a exposé sa pratique dans deux lettres, éditées plusieurs fois outre-Manche. Ses travaux ont influencé l'abbé Charles-Michel de L'Épée, qui a adapté à la langue française sa méthode de démutisation des sourds-muets. Wallis a appliqué aussi la phonétique, dans une optique clinique, aux dyslalies fonctionnelles et à la correction des accents étrangers. Il a eu des échanges épistolaires postérieurs sur ces questions avec un autre précurseur en phonétique et orthophonie : Johann Conrad Amman.