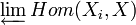Limite inductive - Définition

Avant -propos

L'efficacité du concept de limite en analyse n'est plus à démontrer. L'idée de la limite inductive (et de sa duale, la limite projective) cherche à généraliser à l'algèbre ce qui fonctionne si bien en analyse.

Un premier point clef est la notion de passage à la limite. Une limite de nombres réels positifs est positive. La limite de la racine carrée est égale à la racine carré de la limite. De manière analogue, en algèbre, on va chercher quelles sont les propriétés qui passent à la limite (inductive, projective ou les deux). Ces propriétés ne seront pas des fonctions comme en analyse mais des foncteurs. Ainsi, un foncteur covariant compatible avec la limite inductive fera en sorte que la limite inductive des images est égale à l'image de la limite inductive. (Si le foncteur est contravariant, il transformera une limite inductive en limite projective.)

Par exemple, dans la catégorie des modules sur un anneau commutatif A. La limite inductive existe toujours, elle est compatible avec le noyau, l'image et le conoyau. Par contre, la limite projective est compatible avec le noyau mais pas avec l'image.

Certaines structures se construisent naturellement par passage à la limite. Pour une extension algébrique infinie, le groupe de galois peut se définir par limite projective. On obtient ainsi un groupe profini.

Un deuxième point clef est la notion de densité. Tout nombre réel est limite de nombres rationnels et même de nombres décimaux, ce qui est la base de la manipulation des nombres à l'aide des calculatrices. Toute fonction continue définie sur un segment est limite uniforme de fonctions polynomiales, et même de fonctions en escalier. Ce résultat permet par exemple une démonstration fulgurante du théorème de Riemann-Lebesgue. On démontre d'abord le résultat pour les fonctions en escaliers et ensuite on passe à la limite. C'est cet état d'esprit que l'on va cherche à reproduire en algèbre grâce aux limites inductives. Au lieu de démontrer directement un résultat, on commence par le démontrer sur des objets simples puis on passe à la limite inductive. On peut remarquer par exemple que tout espace vectoriel est limite inductive d'espaces vectoriels de dimension finie.

Système inductif

Soit un ensemble ordonné filtrant. Soit C une catégorie. On appelle système inductif d'objets de C indexés par I la donnée d'une famille d'objets de C et de morphismes pour chaque couple d'indices tel que ; le tout vérifiant :

• 
• .

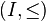
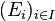
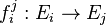
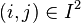
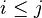
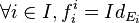
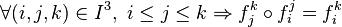
Ensemble ordonné filtrant

Soit un ensemble ordonné (partiellement ordonné en général). On dit que est un ensemble ordonné filtrant ssi

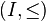
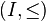
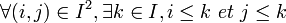
On dit qu'un ensemble est filtrant à gauche lorsque l'ordre opposé est filtrant. Dans un tel cas, on conservera le vocabulaire mais il correspondra à l'ordre opposé. Dans la pratique, cela n'engendre pas de confusion, c'est même plutôt pratique.

Construction de la limite inductive

La limite inductive existe dans la plupart des catégories usuelles (notamment les magmas, monoîdes, groupes, groupes abéliens, anneaux, A-modules, K-espaces vectoriels, espaces topologiques, etc.). On peut la construire à partir de la limlite inductive de la famille d'ensembles sous-jacents. Elle commute donc avec le foncteur d'oubli.

De façon plus générale, dans une catégorie quelconque, sa construction est duale de celle de limite projective. On construit la limite projective à l'aide de deux processus, celui de produit et celui de noyau. On construit la limite inductive à partir des deux notions duales de somme et de conoyau.

Propriété universelle de la limite inductive

Soit (X_i, f_ij) un système inductif dans une catégorie C . La limite inductive X, lorsqu'elle existe est un objet de la catégorie C muni de flèches φ_i de X_i à valeurs dans X vérifiant les relations de compatibilité pour tous . De plus, la donnée (X,φ_i) doit être universelle : pour tout autre objet Y muni d'une famille de flèches ψ_i vérifiant des compatibilités analogues, il existe une unique flèche u : X → Y telle que le diagramme :

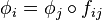
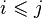
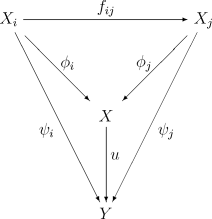
soit commutatif pour tous i ≤ j. La limite inductive est notée : . On parlera de limite inductive des X_i suivant les morphismes de transition f_ij, ou par abus de langage, de limite suivant I, voir tout simplement de limite inductive des X_i.

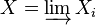
Comme pour toute propriété universelle, lorsqu'elle existe, la limite inductive est unique, à isomorphisme unique près.

Autrement dit, la limite inductive représente le foncteur qui à un objet Y de la catégorie C associe l'ensemble .