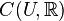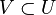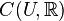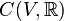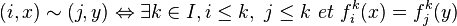Limite inductive - Définition

Limite inductive d'espace topologiques

Soit (E_i, f_ij) un système inductif d'espaces topologiques. On munit successivement la réunion disjointe des ensemble sous-jacent puis l'espace quotient de la topologie quotient dans la construction précédente.

Limite inductive d'ensemble

Soit (E_i, f_ij) un système inductif d'ensembles. On obtient la limite inductive comme quotient de l'union disjointe par la relation d'équivalence :

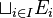
Notons l'ensemble quotient. Pour définir , on prend comme φ_i(x) la classe de (i,x).

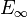
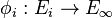
Propriétés

• Si chaque loi * _i est commuative, alors la loi * est commutative.
• Si chaque loi * _i est associative, alors la loi * est associative.
• Si chaque loi * _i possède un neutre e_i et si chaque morphisme vérifie , alors * possède un neutre e (De plus, pour chaque i, on a φ_i(e_i) = e).
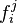
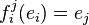
• Si chaque E_i possède une structure de groupe, est un groupe.

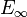
Limite inductive de magmas

Soit (E_i, f_ij) un système inductif de magmas. Chaque ensemble E_i est muni d'une loi de composition interne * _i et chaque application est un morphisme. On commence par construire la limite inductive des ensembles E_i. Il existe alors une unique structure de magma sur telle que les applications canonique φ_i soient des morphimes.

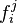
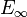
On construit cette loi de la façon suivante. Soit (i,x) et (j,y) deux représentants de deux éléments de . Il existe tel que et . Dans , on a et . On pose alors , le résultat obtenu ne dépend bien sur pas du choix de k.

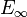
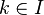
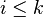
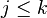
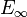
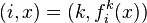
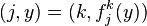
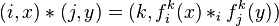
Limite inductive de modules

Soit A un anneau commutatif et (E_i, f_ij) un système inductif de A-modules. On peut munit la limite inductive des ensembles sous-jacent d'une structure de A-module de sorte que les application φ_i soient linéaire. une telle structure est unique et se construit de la même façon que pour les magmas.

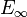
Limite inductive d'anneaux

De façon analogue, si chaque ensemble E_i est muni de deux lois + _i et * _i, la limite inductive est munie de deux lois + et * . Si chaque loi * _i est distributive par rapport à + _i, alors * est distributive est par rapport à + .

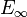
Ce procédé permet ainsi de construire une limite inductive d'anneau.

• Si chaque anneau E_i est intègre, il en est de même de .
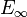
• Si chaque anneau E_i est un corps, il en est de même de .

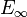
Exemples

• Si l'ensemble filtrant I est fini, il possède un plus grand élément ω. La limite inductive de tout système inductif est alors égale à E_ω. Si I est infini mais possède un plus grand élément quand même, le résultat est le même.
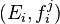
• Soit E un ensemble et (E_n) une suite croissante de sous-ensembles de E, avec les injections canoniques. la limite inductive de la suite (E_n) s'identifie à la réunion de ces ensembles.

• Soit p un nombre premier. Pour tout n soit U_n le groupe cyclique des racines pⁿ-ièmes de l'unité dans un corps algébriquement clos. On considère les inclusions comme morphismes de transition. La limite directe de ce système est alors le groupe infini constitué de toutes les racines p-primaires de l'unité.

• Soit E un espace topologique et a un point de E le germe des fonctions E dans est la limite inductive des ensembles des ensembles des applications continues d'un voisinages quelconques U de a. Les voisinages étant ordonné par l'inclusion (filtante à gauche, ce qui inverse le sens des flèches). Pour , on va de dans par restriction.