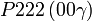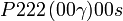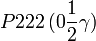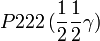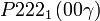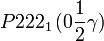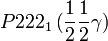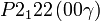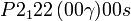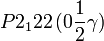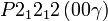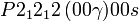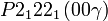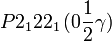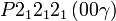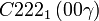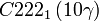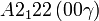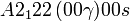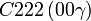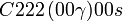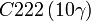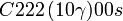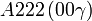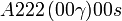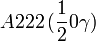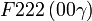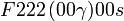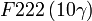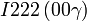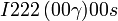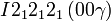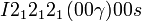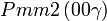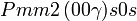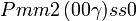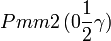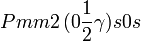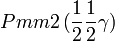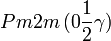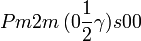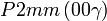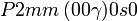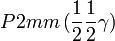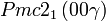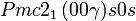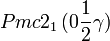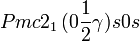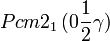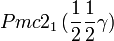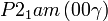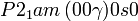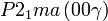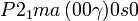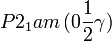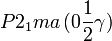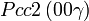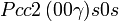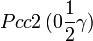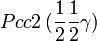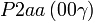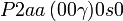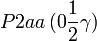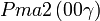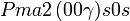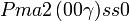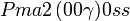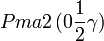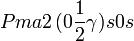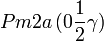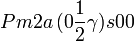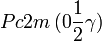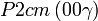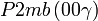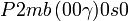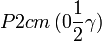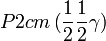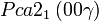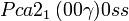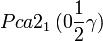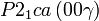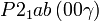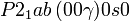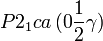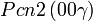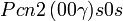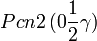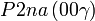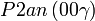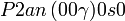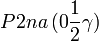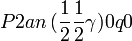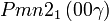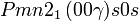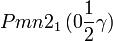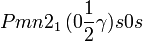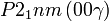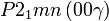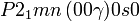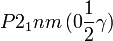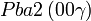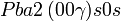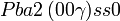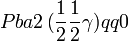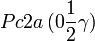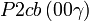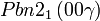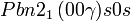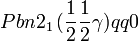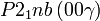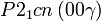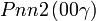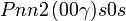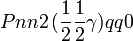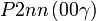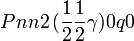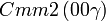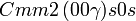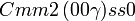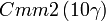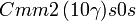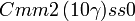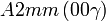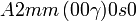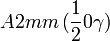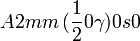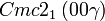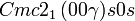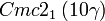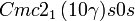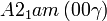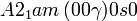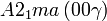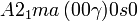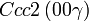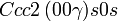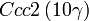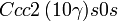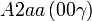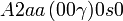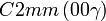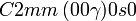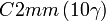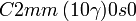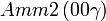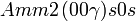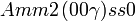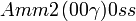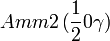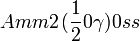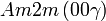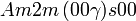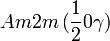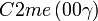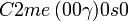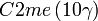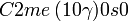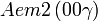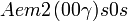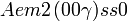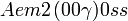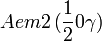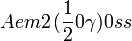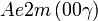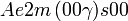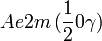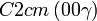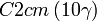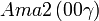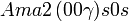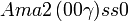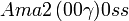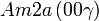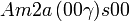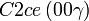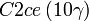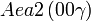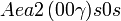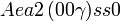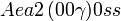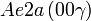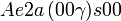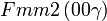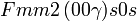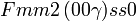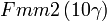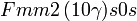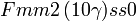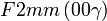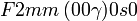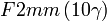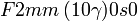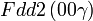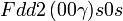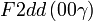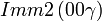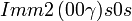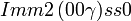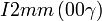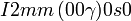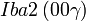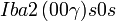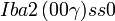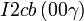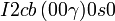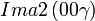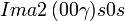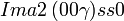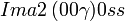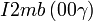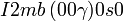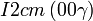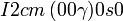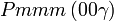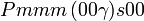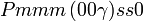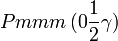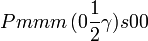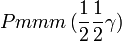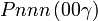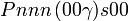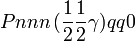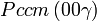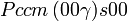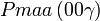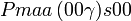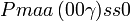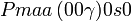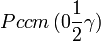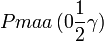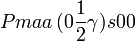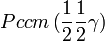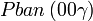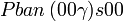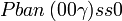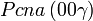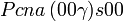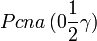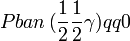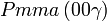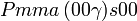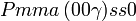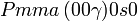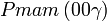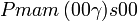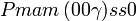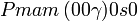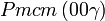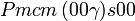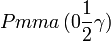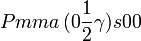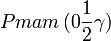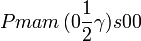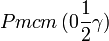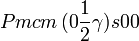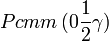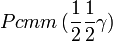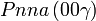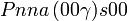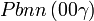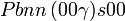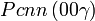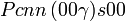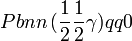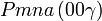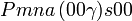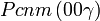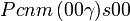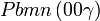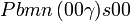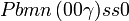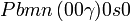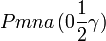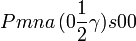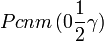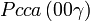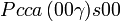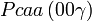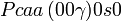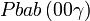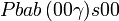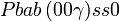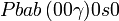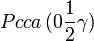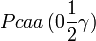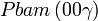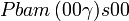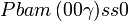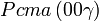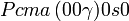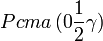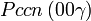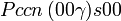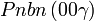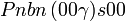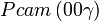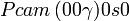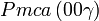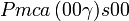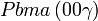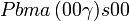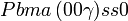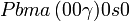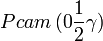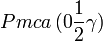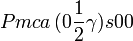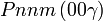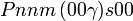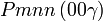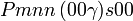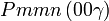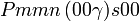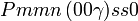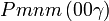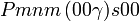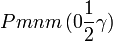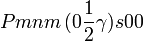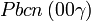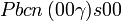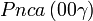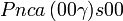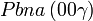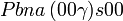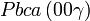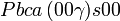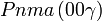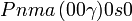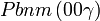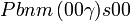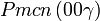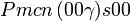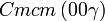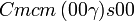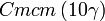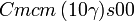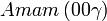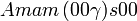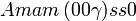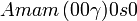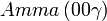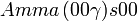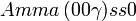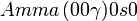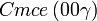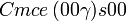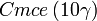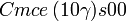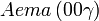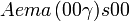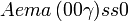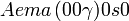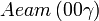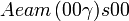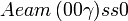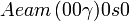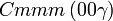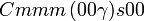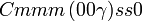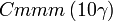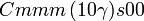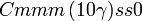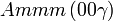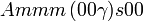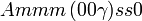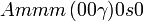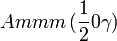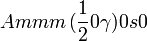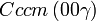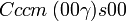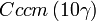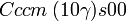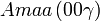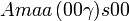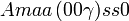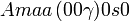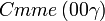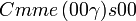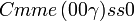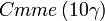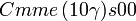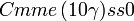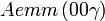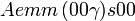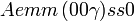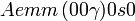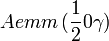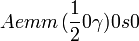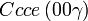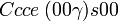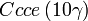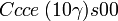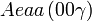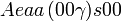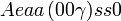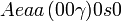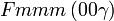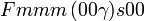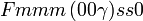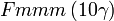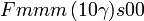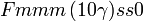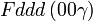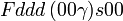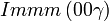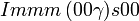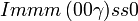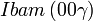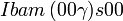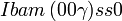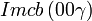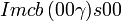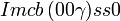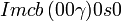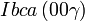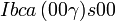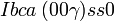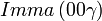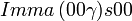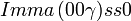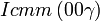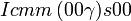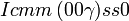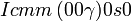Liste des groupes d'espace (3+1)D (orthorhombique) - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

Pour des raisons de taille, la liste des groupes d'espace (3+1)D de l'article groupe d'espace (4D) est scindée en quatre pages :

liste des groupes d'espace (3+1)D (triclinique, monoclinique) ;
liste des groupes d'espace (3+1)D (orthorhombique) ;
liste des groupes d'espace (3+1)D (quadratique) ;
liste des groupes d'espace (3+1)D (trigonal, hexagonal).

Cette page liste les groupes d'espace (3+1)D (orthorhombique).

Système orthorhombique
	$P222\,(00\gamma)$	$P222\,(00\gamma)00s$	$P222\,(0\frac{1}{2}\gamma)$	$P222\,(\frac{1}{2}\frac{1}{2}\gamma)$	$P222_1\,(00\gamma)$
	$P222_1\,(0\frac{1}{2}\gamma)$	$P222_1\,(\frac{1}{2}\frac{1}{2}\gamma)$	$P2_122\,(00\gamma)$	$P2_122\,(00\gamma)00s$	$P2_122\,(0\frac{1}{2}\gamma)$
	$P2_12_12\,(00\gamma)$	$P2_12_12\,(00\gamma)00s$	$P2_122_1\,(00\gamma)$	$P2_122_1\,(0\frac{1}{2}\gamma)$	$P2_12_12_1\,(00\gamma)$
	$C222_1\,(00\gamma)$	$C222_1\,(10\gamma)$	$A2_122\,(00\gamma)$	$A2_122\,(00\gamma)00s$	$C222\,(00\gamma)$
	$C222\,(00\gamma)00s$	$C222\,(10\gamma)$	$C222\,(10\gamma)00s$	$A222\,(00\gamma)$	$A222\,(00\gamma)00s$
	$A222\,(\frac{1}{2}0\gamma)$	$F222\,(00\gamma)$	$F222\,(00\gamma)00s$	$F222\,(10\gamma)$	$I222\,(00\gamma)$
	$I222\,(00\gamma)00s$	$I2_12_12_1\,(00\gamma)$	$I2_12_12_1\,(00\gamma)00s$	$Pmm2\,(00\gamma)$	$Pmm2\,(00\gamma)s0s$
	$Pmm2\,(00\gamma)ss0$	$Pmm2\,(0\frac{1}{2}\gamma)$	$Pmm2\,(0\frac{1}{2}\gamma)s0s$	$Pmm2\,(\frac{1}{2}\frac{1}{2}\gamma)$	$Pm2m\,(0\frac{1}{2}\gamma)$
	$Pm2m\,(0\frac{1}{2}\gamma)s00$	$P2mm\,(00\gamma)$	$P2mm\,(00\gamma)0s0$	$P2mm\,(0\frac{1}{2}\gamma)$	$P2mm\,(\frac{1}{2}\frac{1}{2}\gamma)$
	$Pmc2_1\,(00\gamma)$	$Pmc2_1\,(00\gamma)s0s$	$Pmc2_1\,(0\frac{1}{2}\gamma)$	$Pmc2_1\,(0\frac{1}{2}\gamma)s0s$	$Pcm2_1\,(0\frac{1}{2}\gamma)$
	$Pmc2_1\,(\frac{1}{2}\frac{1}{2}\gamma)$	$P2_1am\,(00\gamma)$	$P2_1am\,(00\gamma)0s0$	$P2_1ma\,(00\gamma)$	$P2_1ma\,(00\gamma)0s0$
	$P2_1am\,(0\frac{1}{2}\gamma)$	$P2_1ma\,(0\frac{1}{2}\gamma)$	$Pcc2\,(00\gamma)$	$Pcc2\,(00\gamma)s0s$	$Pcc2\,(0\frac{1}{2}\gamma)$
	$Pcc2\,(\frac{1}{2}\frac{1}{2}\gamma)$	$P2aa\,(00\gamma)$	$P2aa\,(00\gamma)0s0$	$P2aa\,(0\frac{1}{2}\gamma)$	$Pma2\,(00\gamma)$
	$Pma2\,(00\gamma)s0s$	$Pma2\,(00\gamma)ss0$	$Pma2\,(00\gamma)0ss$	$Pma2\,(0\frac{1}{2}\gamma)$	$Pma2\,(0\frac{1}{2}\gamma)s0s$
	$Pm2a\,(0\frac{1}{2}\gamma)$	$Pm2a\,(0\frac{1}{2}\gamma)s00$	$Pc2m\,(0\frac{1}{2}\gamma)$	$P2cm\,(00\gamma)$	$P2mb\,(00\gamma)$
	$P2mb\,(00\gamma)0s0$	$P2cm\,(0\frac{1}{2}\gamma)$	$P2cm\,(\frac{1}{2}\frac{1}{2}\gamma)$	$Pca2_1\,(00\gamma)$	$Pca2_1\,(00\gamma)0ss$
	$Pca2_1\,(0\frac{1}{2}\gamma)$	$P2_1ca\,(00\gamma)$	$P2_1ab\,(00\gamma)$	$P2_1ab\,(00\gamma)0s0$	$P2_1ca\,(0\frac{1}{2}\gamma)$
	$Pcn2\,(00\gamma)$	$Pcn2\,(00\gamma)s0s$	$Pcn2\,(0\frac{1}{2}\gamma)$	$P2na\,(00\gamma)$	$P2an\,(00\gamma)$
	$P2an\,(00\gamma)0s0$	$P2na\,(0\frac{1}{2}\gamma)$	$P2an\,(\frac{1}{2}\frac{1}{2}\gamma)0q0$	$Pmn2_1\,(00\gamma)$	$Pmn2_1\,(00\gamma)s0s$
	$Pmn2_1\,(0\frac{1}{2}\gamma)$	$Pmn2_1\,(0\frac{1}{2}\gamma)s0s$	$P2_1nm\,(00\gamma)$	$P2_1mn\,(00\gamma)$	$P2_1mn\,(00\gamma)0s0$
	$P2_1nm\,(0\frac{1}{2}\gamma)$	$Pba2\,(00\gamma)$	$Pba2\,(00\gamma)s0s$	$Pba2\,(00\gamma)ss0$	$Pba2\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$
	$Pc2a\,(0\frac{1}{2}\gamma)$	$P2cb\,(00\gamma)$	$Pbn2_1\,(00\gamma)$	$Pbn2_1\,(00\gamma)s0s$	$Pbn2_1\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$
	$P2_1nb\,(00\gamma)$	$P2_1cn\,(00\gamma)$	$Pnn2\,(00\gamma)$	$Pnn2\,(00\gamma)s0s$	$Pnn2\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$
	$P2nn\,(00\gamma)$	$Pnn2\,(\frac{1}{2}\frac{1}{2}\gamma)0q0$	$Cmm2\,(00\gamma)$	$Cmm2\,(00\gamma)s0s$	$Cmm2\,(00\gamma)ss0$
	$Cmm2\,(10\gamma)$	$Cmm2\,(10\gamma)s0s$	$Cmm2\,(10\gamma)ss0$	$A2mm\,(00\gamma)$	$A2mm\,(00\gamma)0s0$
	$A2mm\,(\frac{1}{2}0\gamma)$	$A2mm\,(\frac{1}{2}0\gamma)0s0$	$Cmc2_1\,(00\gamma)$	$Cmc2_1\,(00\gamma)s0s$	$Cmc2_1\,(10\gamma)$
	$Cmc2_1\,(10\gamma)s0s$	$A2_1am\,(00\gamma)$	$A2_1am\,(00\gamma)0s0$	$A2_1ma\,(00\gamma)$	$A2_1ma\,(00\gamma)0s0$
	$Ccc2\,(00\gamma)$	$Ccc2\,(00\gamma)s0s$	$Ccc2\,(10\gamma)$	$Ccc2\,(10\gamma)s0s$	$A2aa\,(00\gamma)$
	$A2aa\,(00\gamma)0s0$	$C2mm\,(00\gamma)$	$C2mm\,(00\gamma)0s0$	$C2mm\,(10\gamma)$	$C2mm\,(10\gamma)0s0$
	$Amm2\,(00\gamma)$	$Amm2\,(00\gamma)s0s$	$Amm2\,(00\gamma)ss0$	$Amm2\,(00\gamma)0ss$	$Amm2\,(\frac{1}{2}0\gamma)$
	$Amm2\,(\frac{1}{2}0\gamma)0ss$	$Am2m\,(00\gamma)$	$Am2m\,(00\gamma)s00$	$Am2m\,(\frac{1}{2}0\gamma)$	$C2me\,(00\gamma)$
	$C2me\,(00\gamma)0s0$	$C2me\,(10\gamma)$	$C2me\,(10\gamma)0s0$	$Aem2\,(00\gamma)$	$Aem2\,(00\gamma)s0s$
	$Aem2\,(00\gamma)ss0$	$Aem2\,(00\gamma)0ss$	$Aem2\,(\frac{1}{2}0\gamma)$	$Aem2\,(\frac{1}{2}0\gamma)0ss$	$Ae2m\,(00\gamma)$
	$Ae2m\,(00\gamma)s00$	$Ae2m\,(\frac{1}{2}0\gamma)$	$C2cm\,(00\gamma)$	$C2cm\,(10\gamma)$	$Ama2\,(00\gamma)$
	$Ama2\,(00\gamma)s0s$	$Ama2\,(00\gamma)ss0$	$Ama2\,(00\gamma)0ss$	$Am2a\,(00\gamma)$	$Am2a\,(00\gamma)s00$
	$C2ce\,(00\gamma)$	$C2ce\,(10\gamma)$	$Aea2\,(00\gamma)$	$Aea2\,(00\gamma)s0s$	$Aea2\,(00\gamma)ss0$
	$Aea2\,(00\gamma)0ss$	$Ae2a\,(00\gamma)$	$Ae2a\,(00\gamma)s00$	$Fmm2\,(00\gamma)$	$Fmm2\,(00\gamma)s0s$
	$Fmm2\,(00\gamma)ss0$	$Fmm2\,(10\gamma)$	$Fmm2\,(10\gamma)s0s$	$Fmm2\,(10\gamma)ss0$	$F2mm\,(00\gamma)$
	$F2mm\,(00\gamma)0s0$	$F2mm\,(10\gamma)$	$F2mm\,(10\gamma)0s0$	$Fdd2\,(00\gamma)$	$Fdd2\,(00\gamma)s0s$
	$F2dd\,(00\gamma)$	$Imm2\,(00\gamma)$	$Imm2\,(00\gamma)s0s$	$Imm2\,(00\gamma)ss0$	$I2mm\,(00\gamma)$
	$I2mm\,(00\gamma)0s0$	$Iba2\,(00\gamma)$	$Iba2\,(00\gamma)s0s$	$Iba2\,(00\gamma)ss0$	$I2cb\,(00\gamma)$
	$I2cb\,(00\gamma)0s0$	$Ima2\,(00\gamma)$	$Ima2\,(00\gamma)s0s$	$Ima2\,(00\gamma)ss0$	$Ima2\,(00\gamma)0ss$
	$I2mb\,(00\gamma)$	$I2mb\,(00\gamma)0s0$	$I2cm\,(00\gamma)$	$I2cm\,(00\gamma)0s0$	$Pmmm\,(00\gamma)$
	$Pmmm\,(00\gamma)s00$	$Pmmm\,(00\gamma)ss0$	$Pmmm\,(0\frac{1}{2}\gamma)$	$Pmmm\,(0\frac{1}{2}\gamma)s00$	$Pmmm\,(\frac{1}{2}\frac{1}{2}\gamma)$
	$Pnnn\,(00\gamma)$	$Pnnn\,(00\gamma)s00$	$Pnnn\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$	$Pccm\,(00\gamma)$	$Pccm\,(00\gamma)s00$
	$Pmaa\,(00\gamma)$	$Pmaa\,(00\gamma)s00$	$Pmaa\,(00\gamma)ss0$	$Pmaa\,(00\gamma)0s0$	$Pccm\,(0\frac{1}{2}\gamma)$
	$Pmaa\,(0\frac{1}{2}\gamma)$	$Pmaa\,(0\frac{1}{2}\gamma)s00$	$Pccm\,(\frac{1}{2}\frac{1}{2}\gamma)$	$Pban\,(00\gamma)$	$Pban\,(00\gamma)s00$
	$Pban\,(00\gamma)ss0$	$Pcna\,(00\gamma)$	$Pcna\,(00\gamma)s00$	$Pcna\,(0\frac{1}{2}\gamma)$	$Pban\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$
	$Pmma\,(00\gamma)$	$Pmma\,(00\gamma)s00$	$Pmma\,(00\gamma)ss0$	$Pmma\,(00\gamma)0s0$	$Pmam\,(00\gamma)$
	$Pmam\,(00\gamma)s00$	$Pmam\,(00\gamma)ss0$	$Pmam\,(00\gamma)0s0$	$Pmcm\,(00\gamma)$	$Pmcm\,(00\gamma)s00$
	$Pmma\,(0\frac{1}{2}\gamma)$	$Pmma\,(0\frac{1}{2}\gamma)s00$	$Pmam\,(0\frac{1}{2}\gamma)$	$Pmam\,(0\frac{1}{2}\gamma)s00$	$Pmcm\,(0\frac{1}{2}\gamma)$
	$Pmcm\,(0\frac{1}{2}\gamma)s00$	$Pcmm\,(0\frac{1}{2}\gamma)$	$Pcmm\,(\frac{1}{2}\frac{1}{2}\gamma)$	$Pnna\,(00\gamma)$	$Pnna\,(00\gamma)s00$
	$Pbnn\,(00\gamma)$	$Pbnn\,(00\gamma)s00$	$Pcnn\,(00\gamma)$	$Pcnn\,(00\gamma)s00$	$Pbnn\,(\frac{1}{2}\frac{1}{2}\gamma)qq0$
	$Pmna\,(00\gamma)$	$Pmna\,(00\gamma)s00$	$Pcnm\,(00\gamma)$	$Pcnm\,(00\gamma)s00$	$Pbmn\,(00\gamma)$
	$Pbmn\,(00\gamma)s00$	$Pbmn\,(00\gamma)ss0$	$Pbmn\,(00\gamma)0s0$	$Pmna\,(0\frac{1}{2}\gamma)$	$Pmna\,(0\frac{1}{2}\gamma)s00$
	$Pcnm\,(0\frac{1}{2}\gamma)$	$Pcca\,(00\gamma)$	$Pcca\,(00\gamma)s00$	$Pcaa\,(00\gamma)$	$Pcaa\,(00\gamma)0s0$
	$Pbab\,(00\gamma)$	$Pbab\,(00\gamma)s00$	$Pbab\,(00\gamma)ss0$	$Pbab\,(00\gamma)0s0$	$Pcca\,(0\frac{1}{2}\gamma)$
	$Pcaa\,(0\frac{1}{2}\gamma)$	$Pbam\,(00\gamma)$	$Pbam\,(00\gamma)s00$	$Pbam\,(00\gamma)ss0$	$Pcma\,(00\gamma)$
	$Pcma\,(00\gamma)0s0$	$Pcma\,(0\frac{1}{2}\gamma)$	$Pccn\,(00\gamma)$	$Pccn\,(00\gamma)s00$	$Pnbn\,(00\gamma)$
	$Pnbn\,(00\gamma)s00$	$Pcam\,(00\gamma)$	$Pcam\,(00\gamma)0s0$	$Pmca\,(00\gamma)$	$Pmca\,(00\gamma)s00$
	$Pbma\,(00\gamma)$	$Pbma\,(00\gamma)s00$	$Pbma\,(00\gamma)ss0$	$Pbma\,(00\gamma)0s0$	$Pcam\,(0\frac{1}{2}\gamma)$
	$Pmca\,(0\frac{1}{2}\gamma)$	$Pmca\,(0\frac{1}{2}\gamma)s00$	$Pnnm\,(00\gamma)$	$Pnnm\,(00\gamma)s00$	$Pmnn\,(00\gamma)$
	$Pmnn\,(00\gamma)s00$	$Pmmn\,(00\gamma)$	$Pmmn\,(00\gamma)s00$	$Pmmn\,(00\gamma)ss0$	$Pmnm\,(00\gamma)$
	$Pmnm\,(00\gamma)s00$	$Pmnm\,(0\frac{1}{2}\gamma)$	$Pmnm\,(0\frac{1}{2}\gamma)s00$	$Pbcn\,(00\gamma)$	$Pbcn\,(00\gamma)s00$
	$Pnca\,(00\gamma)$	$Pnca\,(00\gamma)s00$	$Pbna\,(00\gamma)$	$Pbna\,(00\gamma)s00$	$Pbca\,(00\gamma)$
	$Pbca\,(00\gamma)s00$	$Pnma\,(00\gamma)$	$Pnma\,(00\gamma)0s0$	$Pbnm\,(00\gamma)$	$Pbnm\,(00\gamma)s00$
	$Pmcn\,(00\gamma)$	$Pmcn\,(00\gamma)s00$	$Cmcm\,(00\gamma)$	$Cmcm\,(00\gamma)s00$	$Cmcm\,(10\gamma)$
	$Cmcm\,(10\gamma)s00$	$Amam\,(00\gamma)$	$Amam\,(00\gamma)s00$	$Amam\,(00\gamma)ss0$	$Amam\,(00\gamma)0s0$
	$Amma\,(00\gamma)$	$Amma\,(00\gamma)s00$	$Amma\,(00\gamma)ss0$	$Amma\,(00\gamma)0s0$	$Cmce\,(00\gamma)$
	$Cmce\,(00\gamma)s00$	$Cmce\,(10\gamma)$	$Cmce\,(10\gamma)s00$	$Aema\,(00\gamma)$	$Aema\,(00\gamma)s00$
	$Aema\,(00\gamma)ss0$	$Aema\,(00\gamma)0s0$	$Aeam\,(00\gamma)$	$Aeam\,(00\gamma)s00$	$Aeam\,(00\gamma)ss0$
	$Aeam\,(00\gamma)0s0$	$Cmmm\,(00\gamma)$	$Cmmm\,(00\gamma)s00$	$Cmmm\,(00\gamma)ss0$	$Cmmm\,(10\gamma)$
	$Cmmm\,(10\gamma)s00$	$Cmmm\,(10\gamma)ss0$	$Ammm\,(00\gamma)$	$Ammm\,(00\gamma)s00$	$Ammm\,(00\gamma)ss0$
	$Ammm\,(00\gamma)0s0$	$Ammm\,(\frac{1}{2}0\gamma)$	$Ammm\,(\frac{1}{2}0\gamma)0s0$	$Cccm\,(00\gamma)$	$Cccm\,(00\gamma)s00$
	$Cccm\,(10\gamma)$	$Cccm\,(10\gamma)s00$	$Amaa\,(00\gamma)$	$Amaa\,(00\gamma)s00$	$Amaa\,(00\gamma)ss0$
	$Amaa\,(00\gamma)0s0$	$Cmme\,(00\gamma)$	$Cmme\,(00\gamma)s00$	$Cmme\,(00\gamma)ss0$	$Cmme\,(10\gamma)$
	$Cmme\,(10\gamma)s00$	$Cmme\,(10\gamma)ss0$	$Aemm\,(00\gamma)$	$Aemm\,(00\gamma)s00$	$Aemm\,(00\gamma)ss0$
	$Aemm\,(00\gamma)0s0$	$Aemm\,(\frac{1}{2}0\gamma)$	$Aemm\,(\frac{1}{2}0\gamma)0s0$	$Ccce\,(00\gamma)$	$Ccce\,(00\gamma)s00$
	$Ccce\,(10\gamma)$	$Ccce\,(10\gamma)s00$	$Aeaa\,(00\gamma)$	$Aeaa\,(00\gamma)s00$	$Aeaa\,(00\gamma)ss0$
	$Aeaa\,(00\gamma)0s0$	$Fmmm\,(00\gamma)$	$Fmmm\,(00\gamma)s00$	$Fmmm\,(00\gamma)ss0$	$Fmmm\,(10\gamma)$
	$Fmmm\,(10\gamma)s00$	$Fmmm\,(10\gamma)ss0$	$Fddd\,(00\gamma)$	$Fddd\,(00\gamma)s00$	$Immm\,(00\gamma)$
	$Immm\,(00\gamma)s00$	$Immm\,(00\gamma)ss0$	$Ibam\,(00\gamma)$	$Ibam\,(00\gamma)s00$	$Ibam\,(00\gamma)ss0$
	$Imcb\,(00\gamma)$	$Imcb\,(00\gamma)s00$	$Imcb\,(00\gamma)ss0$	$Imcb\,(00\gamma)0s0$	$Ibca\,(00\gamma)$
	$Ibca\,(00\gamma)s00$	$Ibca\,(00\gamma)ss0$	$Imma\,(00\gamma)$	$Imma\,(00\gamma)s00$	$Imma\,(00\gamma)ss0$
	$Icmm\,(00\gamma)$	$Icmm\,(00\gamma)s00$	$Icmm\,(00\gamma)ss0$	$Icmm\,(00\gamma)0s0$

Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭

Le rôle surprenant de la grossesse contre la grippe A 🦠

Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️

Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋

Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬

Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️

Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️

Ce nouveau type de moteur repousse les limites du vol supersonique ✈️

Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠

Une super-Terre entre Mars et Jupiter ? 🌎

Découverte impressionnante d'un fossile de crocodile géant 🐊

Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡

Un virage technologique révèle l'impact du diabète gestationnel 🩺

Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼

Ce fin gilet robotisé soulage les tâches répétitives 🦾

Les équations d'Einstein invalidées ? 👀

Ce tatouage électronique se connecte à votre cerveau 🧠

Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️

Des plats au bœuf... sans bœuf ? 🥩

Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍

Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️

Découverte: d'autres univers plus propices à la vie que le notre 👽

Ces sons urbains qui minent notre santé mentale 🚗

La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥

Des microalgues éliminent les métaux lourds: voici comment 🧪

Et voici un qubit mécanique ! 🖥️

Les lentilles de contact sont-elles vraiment sans danger ? 👁️

Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥

Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠

Cette astuce quotidienne ajoute 11 ans à votre vie 🕒

Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋

Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀

Voici pourquoi l'alcool peut rendre agressif 🥂

Expérience inédite: ce laser projette une ombre visible 💥

Ce plat millénaire réduit significativement la graisse corporelle 🍽️

Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭

Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠

De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽

Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️

Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐

Une montagne d'or découverte en Chine ⛏️

Cette simulation de l'Univers est totalement vertigineuse 🌀

Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘

Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️

Voici pourquoi votre enfant triche et ce que cela révèle 🧠

Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱

Neuralink: un bras robotique contrôlé par la pensée 🦾

Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀

L'étonnant impact du froid sur notre sommeil ❄️

Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️

Page générée en 2.178 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise