Liste des petits groupes - Définition

Petits groupes abéliens

Les groupes abéliens finis ont une classification simple : ils sont cycliques, ou produits directs de groupes cycliques. Voir l'article détaillé Groupes abéliens.

Ordre	Groupe	Sous-groupes	Propriétés	Graphe des cycles
1	groupe trivial = Z1 = S1 = A2	-	de nombreuses propriétés triviales
2	Z2 = S2 = D1	-	simple, plus petit groupe non trivial
3	Z3 = A3	-	simple
4	Z4	Z2
	groupe de Klein = Z2 × Z2 = D2	Z2 (3)	plus petit groupe non cyclique
5	Z5	-	simple
6	Z6 = Z3 × Z2	Z3 , Z2
7	Z7	-	simple
8	Z8	Z4 , Z2
	Z4 × Z2	Z22, Z4 (2), Z2 (3)
	Z23	Z22 (7) , Z2 (7)	les éléments autres que l'identité correspondent aux points du plan de Fano (en) (le plus petitplan projectif fini), les Z2 × Z2 sous-groupes aux droites de ce plan
9	Z9	Z3
	Z32	Z3 (4)
10	Z10 = Z5 × Z2	Z5 , Z2
11	Z11	-	simple
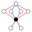
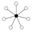
12	Z12 = Z4 × Z3	Z6 , Z4 , Z3 , Z2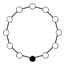
	Z6 × Z2 = Z3 × Z22	Z6 (3), Z3, Z2 (3), Z22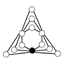
13	Z13	-	simple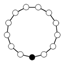
14	Z14 = Z7 × Z2	Z7 , Z2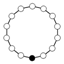
15	Z15 = Z5 × Z3	Z5 , Z3
16	Z16	Z8 , Z4 , Z2
	Z24	Z2 (15) , Z22 (35) , Z23 (15)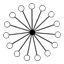
	Z4 × Z22	Z2 (7) , Z4 (4) , Z22 (7) , Z23, Z4 ×Z2 (6)	ce groupe a le même graphe des cycles que celui engendré par les matrices de Pauli (mais ne lui est pas isomorphe)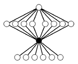
	Z8 × Z2	Z2 (3) , Z4 (2) , Z22, Z8 (2) , Z4 × Z2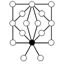
	Z42	Z2 (3), Z4 (6) , Z22, Z4 × Z2 (3)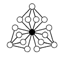
17	Z17	-	simple	Fichier:GroupDiagramMiniC17.png