Graphe des cycles - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, et plus particulièrement en théorie des groupes, le graphe des cycles d'un groupe représente l'ensemble des cycles de ce groupe, ce qui est particulièrement utile pour visualiser la structure des petits groupes finis. Pour les groupes ayant moins de 16 éléments, le graphe des cycles détermine le groupe à isomorphisme près.
Cycles
Un cycle est l'ensemble des puissances d'un élément donné du groupe ; an, la n-ème puissance de l'élément a, est définie comme le produit de a par lui-même n fois (avec les conventions a1 = a et a0 = e, l'élément neutre du groupe). On dit que l'élément a engendre le cycle. Si le groupe est fini, une des puissances (non nulle) doit être l'élément neutre, e ; la plus petite de ces puissances est l’ordre du cycle, c'est-à-dire le nombre d'éléments distincts qu'il contient. Le graphe des cycles est une représentation des cycles par un ensemble de polygones, chaque sommet représentant un élément, et les côtés (reliant les puissances successives) indiquant que tous les éléments du polygone appartiennent au même cycle.
Les cycles peuvent se chevaucher, ou n'avoir que l'élément neutre en commun. Le graphe ne représente que les cycles intéressants.
Si par exemple a engendre un cycle d'ordre 6 (on dit plus simplement que a est d'ordre 6), alors a6 = e. L'ensemble des puissances de a², {a², a4, e} est alors aussi un cycle, mais cela n'apporte aucune information nouvelle. De même, a5 engendre le même cycle que a.
Ainsi, il suffit de considérer les cycles primitifs, ceux qui ne sont sous-ensembles d'aucun autre cycle. Chacun d'eux est engendré par un élément primitif, a. Le graphe des cycles est obtenu en représentant chaque élément du groupe par un sommet, en reliant e à chaque élément primitif a , puis a à a², ... an-1 à an, ... jusqu'à revenir à e.
Techniquement, la description précédente amènerait les éléments d'ordre 2 (tels que a² = e) à être reliés à e par deux arêtes, mais il est conventionnel de n'en dessiner qu'une.
Autres informations lisibles sur le graphe des cycles
- L'inverse d'un élément x est identifiable dans le graphe des cycles : c'est l'élément d'un cycle contenant x dont la distance à e est la même (en parcourant le cycle dans la direction opposée).
Propriétés
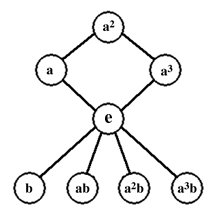
Comme exemple de graphe des cycles, considérons le groupe diédral D4. La table de multiplication de ce groupe est donnée à gauche, et le graphe des cycles est représenté à droite, e étant l'élément neutre.
-
e b a a² a³ ab a²b a³b e e b a a² a³ ab a²b a³b b b e a³b a²b ab a³ a² a a a ab a² a³ e a²b a³b b a² a² a²b a³ e a a³b b ab a³ a³ a³b e a a² b ab a²b ab ab a b a³b a²b e a³ a² a²b a²b a² ab b a³b a e a³ a³b a³b a³ a²b ab b a² a e
On remarque le cycle e, a, a², a³, qui est d'ailleurs aussi un cycle dans l'autre direction : (a³)²=a² , (a³)³=a et (a³)4=e. Ce comportement est général : un cycle peut toujours être parcouru dans les deux sens.
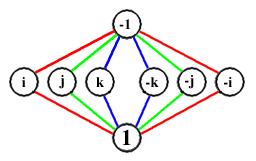
Des ambiguïtés peuvent survenir lorsque deux cycles partagent un élément (autre que l'élément neutre). Considérons par exemple le groupe de quaternions, dont le graphe des cycles est représenté à droite (avec 1 comme élément neutre). Chacun des éléments autres que 1 et -1, représentés dans la rangée centrale, a pour carré -1. Dans ce cas on peut utiliser plusieurs couleurs pour distinguer les cycles, ou choisir une représentation symétrique.
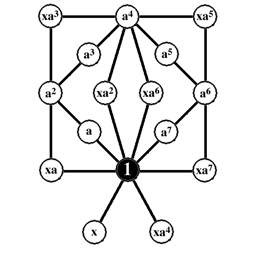
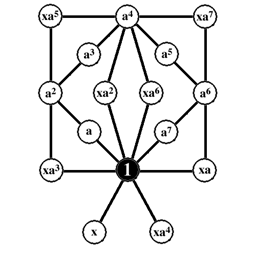
Deux groupes distincts peuvent avoir le même graphe des cycles, et ne peuvent être distingués que par leur table de multiplication, ou en marquant les sommets du graphe à l'aide des générateurs du groupe. Le plus petit ordre pour lequel cela peut se produire est 16 ; les deux groupes Z2 x Z8 et le groupe modulaire, ont même graphe, comme on le voit ci-dessous.