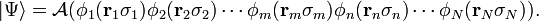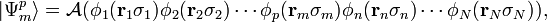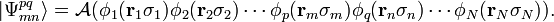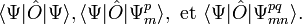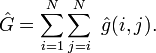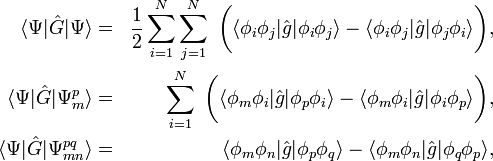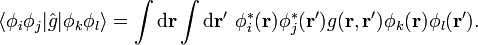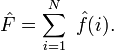Lois de Slater-Condon - Définition

Introduction

En chimie numérique, les lois de Slater-Condon indiquent les intégrales des opérateurs à un ou deux corps sur les fonctions d'onde construites comme des déterminants de Slater d'orbitales orthonormées en termes d'orbitales individuelles. Ce faisant, les intégrales originelles portant sur des fonctions d'ondes à N électrons sont réduites à des sommes sur des intégrales sur au plus deux orbitales molécules, ou, en d'autres termes, l'intégrale originelle 3 N-dimensionnelle est exprimée en termes d'intégrales tri- ou hexadimensionnelles.

Ces lois sont utilisées pour la dérivation des équations fonctionnant pour toutes les méthodes de résolutions approchées de l'équation de Schrödinger employant des fonctions d'ondes construites à partir de déterminants de Slater. Cela inclut la méthode Hartree-Fock, où la fonction d'onde est un déterminant simple, et toutes les méthodes qui se basent sur la méthode Hartree-Fock comme référence comme la théorie de la perturbation de Møller-Plesset, et les théories de cluster couplé ou d'interaction de configuration.

Les lois de Slater-Condon ne s'appliquent que pour des orbitales orthonormées. La généralisation aux orbitales non orthogonales fut proposée par Per-Olov Löwdin, conduisant à ce qui est connu sous la dénomination de lois de Löwdin.

Base

En termes d'un opérateur d'antisymétrisation ( ) agissant sur un produit de N spinorbitales orthonormales (avec r et σ indiquant les variables d'espace et de spin), une fonction d'onde de déterminant s'écrit comme :

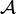
Une fonction d'onde différant de la précédente par une seule orbitale (la m-ième) serait alors notée :

et une fonction d'onde différant de deux orbitales sera écrite :

Pour tout opérateur à un ou deux corps, Ô, les lois de Slater-Condon indiquent la manière de simplifier les types d'intégrales suivants :

Les éléments de matrice pour deux fonctions d'ondes différant par plus de deux orbitales disparaissent sauf si des interactions d'ordres plus importants sont introduites.

John Slater établit à l'origine les expressions pour des éléments de matrice diagonaux d'un hamiltonien approché alors qu'il étudiait les spectres atomiques par une approche perturbative. L'année suivante, Edward Condon étendit les lois aux éléments de matrice non diagonaux. Per-Olov Löwdin généralisa plus tard ces résultats por des fonctions d'ondes construites à partir d'orbitales non-orthonormées.

Intégrales d'opérateurs à deux corps

Les opérateurs à deux corps couplent deux particules à tout instant donné. On peut citer comme exemples les opérateurs de répulsion électron-électron, de couplage magnétique dipolaire ou de moment angulaire total au carré.

Un opérateur à deux corps dans un système à N particules se décompose en :

Les règles de Slater-Condon pour un tel opérateur sont :

où

Intégrales d'opérateurs à un corps

Les opérateurs à un corps dépendent seulement de la position ou de la quantité de mouvement d'un seul électron à un instant donnée. On peut citer comme exemple les opérateurs d'énergie cinétique, de moment dipolaire, et de couplage de moment angulaire.

Un opérateur à un corps dans un système à N particules se décompose en :

Les lois de Slater-Condon pour un tel opérateur sont :