Moment angulaire - Définition

Introduction

Un gyroscope tournant sur un clou

En physique, le moment angulaire ou moment cinétique est la grandeur physique qui joue un rôle analogue à la quantité de mouvement dans le cas des rotations. Comme le moment angulaire dépend du choix de l'origine (ainsi que du référentiel d'étude (R)), il faut toujours spécifier cette origine et ne jamais combiner des moments angulaires ayant des origines différentes.

Cas d'un point matériel

On appelle point matériel ou corps ponctuel un système mécanique dont les dimensions sont petites devant les distances caractéristiques du mouvement étudié (distance parcourue, rayon d'une orbite...). Le système mécanique est alors modélisé par un point géométrique M auquel est associé sa masse m.

Définition

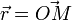
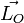
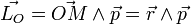
Pour un point matériel M de vecteur position , le moment cinétique ou angulaire par rapport à l'origine O est défini par :

, (1)

où est la quantité de mouvement de la particule. Le moment cinétique est donc le moment de cette dernière par rapport à O. est l'opérateur produit vectoriel.

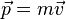
Un exemple simple est celui d'une particule décrivant un cercle de centre O et de rayon r : est dirigé selon l'axe du disque et vaut . Le sens du vecteur moment cinétique ne recouvre pas une réalité physique mais est une convention ; c'est un vecteur axial.

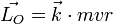
Par analogie avec la quantité de mouvement, le moment cinétique permet de définir l'analogue de la masse : le moment d'inertie I. En effet : , avec I = mr², et où est la vitesse angulaire du point M, à laquelle on peut faire correspondre le vecteur axial . Le moment cinétique s'écrit finalement :

.

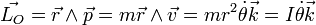
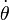
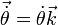
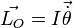
Théorème du moment cinétique pour un point matériel

Si l'on dérive membre à membre la définition (1) du moment angulaire, il vient, en supposant O fixe dans (R): , puisque et sont colinéaires.

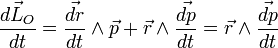
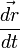
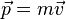
Par ailleurs pour un corps ponctuel, on a (relation fondamentale de la dynamique):

, (2), le terme de droite correspondant à la somme des forces (réelles ou "d'inertie") exercées sur le corps.

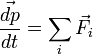
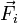
Par suite il vient l'équation suivante, dite théorème du moment cinétique:

, (3)

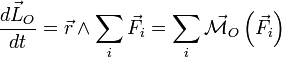
où est le moment de la force par rapport au point O.

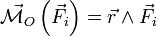
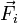
Remarque: par rapport à un point O mobile dans (R), le théorème du moment cinétique s'écrit: .
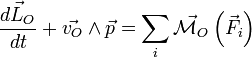
La seule différence vient de l'addition d'un terme complémentaire dans le membre de gauche de la relation (3).

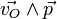
Cas d'un système matériel

Définition dans le cas général

Si un système est constitué de plusieurs particules (modèle discret), le moment angulaire total est obtenu en additionant ou intégrant le moment angulaire de chacun de ses constituants. Il est également possible de se placer dans la limite des milieux continus pour décrire certains systèmes mécaniques (solides, notamment).

Suivant que l'on adopte un modèle discret ou continu, le moment cinétique du système (S) par rapport à un point O s'écrit :

ou

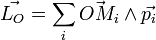
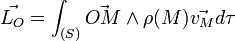
Ces expressions générales ne sont guère utilisables directement. Le théorème de Koenig relatif au moment cinétique permet d'en donner une forme plus compréhensible physiquement.

Dans le cas d'un système à constante (cas des solides notamment), on peut aussi écrire :

où ou .

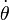
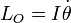
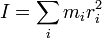
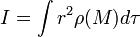
Théorème de Koenig pour le moment cinétique

Soit G le centre d'inertie du système, M la masse totale du système alors :

.

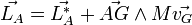
Le moment cinétique d'un système fermé en un point est égal au moment cinétique en ce point du centre d'inertie G affecté de la masse totale, augmenté du moment cinétique barycentrique.

Remarque : Si A est en G alors . On a donc une égalité de moment cinétique malgré la différence de référentiel (galiléen et barycentrique) et donc de vitesse associée.

Cas d'un solide: tenseur d'inertie