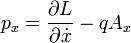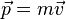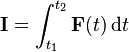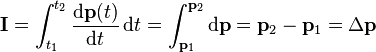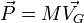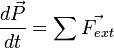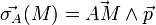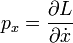Quantité de mouvement - Définition

Introduction

En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et à la masse d'un objet. Elle fait partie, avec l'énergie, des valeurs qui se conservent lors des interactions entre éléments du système. Cette loi, d'abord empirique, a été expliquée par le théorème de Noether et est liée à la symétrie des équations de la physique par translation dans l'espace.

Quantité de mouvement et impulsion sont souvent confondues en raison de leur coïncidence dans la majorité des cas. Néanmoins en théorie ces deux grandeurs sont distinctes.

En mécanique classique

En mécanique classique, la quantité de mouvement d'un point matériel de masse animé d'une vitesse est définie comme produit de la masse et de la vitesse :

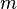
C'est donc, comme la vitesse, une grandeur vectorielle.

L'unité SI de la quantité de mouvement est le kg   m   s^-1.

Variation de quantité de mouvement

Une variation de quantité de mouvement consécutive à l'action d'une force est calculée comme étant l'intégrale de la force pendant la durée d'action de la force. Pour la calculer, considérons un objet de quantité de mouvement initiale à un instant t₁. Cet objet subit une force pendant une durée t₂ − t₁. L'intégrale de cette force par rapport au temps, pendant cette durée, est égale à :

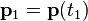
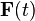
En utilisant la définition de la force , on obtient :

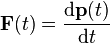
L'usage, dérivé de l'appellation anglo-saxonne impulse, est d'appeler cette grandeur impulsion. Néanmoins, en toute rigueur, en français impulsion désigne le moment linéaire, grandeur de la mécanique lagrangienne. Lorsque la durée d'action de la force est très courte, la grandeur I précédente est appelée percussion mécanique, en raison de son importance dans la théorie des chocs.

Théorème du centre d'inertie pour un système

En mécanique classique, l'application des lois de Newton permet de démontrer le théorème du centre d'inertie qui apparaît comme la généralisation de la seconde loi de Newton pour un système quelconque (solide ou ensemble de points matériels, ensemble de solides) :

Si désigne la masse totale du système et son centre d'inertie, alors, la quantité de mouvement du système (ou résultante cinétique) est :

désignant donc la vitesse du centre d'inertie du système et M la masse totale du système.

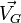
Le théorème s'énonce alors ainsi : la variation de la quantité de mouvement du système est égale à la somme des forces extérieures s'exerçant sur le système :

Cette relation est fondamentale : c'est elle qui permet d'étudier le mouvement d'un solide sans avoir besoin de connaître les forces de liaison interatomique. Elle sert à étudier autant la chute d'une pomme que le mouvement de la Lune autour de la Terre.

Un cas particulier important : si l'on imagine le choc de deux objets (ou particules) pour lequel la somme des forces extérieures (au système constitué de ces 2 objets) est nulle (ou négligeable), alors la quantité de mouvement totale se conserve : elle est la même après le choc qu'avant le choc, et ce en dépit des interactions qui ont eu lieu pendant le choc. C'est d'ailleurs l'étude des chocs qui a conduit Descartes à penser qu'une certaine quantité du mouvement était nécessairement conservée.

Moment cinétique

Le moment cinétique d'un point M materiel de masse m et de vitesse v en un point A peut s'exprimer ainsi: soit:

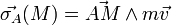
En mécanique lagrangienne

En mécanique lagrangienne, si l'on note le lagrangien du système avec une coordonnée de position du système et sa dérivée par rapport au temps, on obtient la composante de la quantité de mouvement suivant la direction x par :

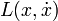
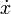
Cette relation, qui en réalité définit le moment conjugué de la position (ou impulsion), n'est toutefois pas générale. Dans le cas notamment d'une particule chargée en mouvement dans un champ électromagnétique la quantité de mouvement est définie par :

où q est la charge électrique de la particule et A est le potentiel vecteur.