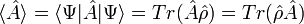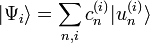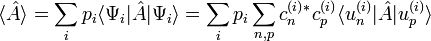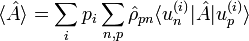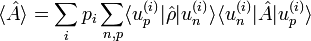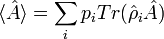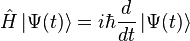Matrice densité - Définition

Propriété

La matrice obtenue a les propriétés suivantes :

• Elle est hermitienne, , elle peut donc être diagonalisée, et ses valeurs propres sont positives.
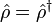
• Sa trace est égale à 1, , conservation de la probabilité totale.
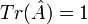
• Elle doit être définie positive ou nulle.
• Dans le cas d'un état pur, l'opérateur densité est alors un projecteur : .
• , avec égalité si et seulement si le système physique est dans un état pur (c'est-à-dire que tous les p_i sont nuls sauf un).

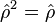
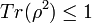
Valeur moyenne

On peut calculer la valeur moyenne d'une observable A à partir de la formule :

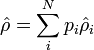
avec est la matrice densité d'un mélange statistique d'états.

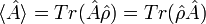
Evolution avec le temps

L'évolution temporelle du vecteur d'état est donné par l'équation de Schrödinger dépendante du temps :