Observable - Définition et Explications

Introduction

Dans le formalisme de la mécanique quantique, une opération de mesure (c'est-à-dire obtenir la valeur ou un intervalle de valeurs d'un paramètre physique, ou plus généralement une information sur un système physique) est représentée par ce qu'il est convenu d'appeler une observable.

Définition formelle

Une observable est formalisée mathématiquement par un opérateur (Le mot opérateur est employé dans les domaines :) agissant sur les vecteurs d'un espace de Hilbert (Un espace de Hilbert est un espace de Banach (donc complet) dont la norme découle d'un produit scalaire ou hermitien par la formule . C'est la généralisation en dimension quelconque d'un espace euclidien...) (chaque état quantique (En mécanique quantique, l'état d'un système décrit tous les aspects du système physique. Il est représenté par un objet mathématique qui donne le maximum d'information possible sur le système, dans le but de...) étant représenté par un vecteur (En mathématiques, un vecteur est un élément d'un espace vectoriel, ce qui permet d'effectuer des opérations d'addition et de multiplication par un scalaire. Un...) dans cet espace).

Le sens (SENS (Strategies for Engineered Negligible Senescence) est un projet scientifique qui a pour but l'extension radicale de l'espérance de vie humaine. Par une...) de cet opérateur observable est de donner la possibilité de décomposer un état quantique quelconque (donc un vecteur quelconque de l'espace de Hilbert) en une combinaison (Une combinaison peut être :) linéaire d'états propres, chacun de ces états étant un état possible résultant de l'opération de mesure.

Soient les vecteurs propres de (éventuellement en nombre (La notion de nombre en linguistique est traitée à l’article « Nombre grammatical ».) infini (Le mot « infini » (-e, -s ; du latin finitus, « limité »), est un adjectif servant à qualifier quelque chose qui n'a pas de limite en nombre ou en...) selon l'observable).

étant le coefficient (En mathématiques un coefficient est un facteur multiplicatif qui dépend d'un certain objet, comme une variable (par exemple, les coefficients d'un polynôme), un espace vectoriel, une fonction de base et ainsi de suite....) complexe de cette combinaison linéaire.

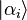
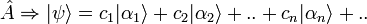
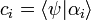
Ce coefficient donne la probabilité (La probabilité (du latin probabilitas) est une évaluation du caractère probable d'un évènement. En mathématiques, l'étude des probabilités est un sujet de...) pour qu'un état propre soit le résultat de la mesure d'un état quantique  :

(en supposant que et soient normés)

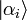
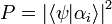
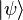
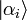
L'ensemble (En théorie des ensembles, un ensemble désigne intuitivement une collection d’objets (les éléments de l'ensemble), « une multitude qui peut être comprise comme un...) des vecteurs propres n'est autre que l'ensemble des résultats possibles de l'opération de mesure formalisée par l'observable.

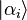
Les états qui s'expriment avant la mesure sous la forme simple sont appelés état propre ou état pur. En règle générale, un état quantique n'est pas pur et sont des états superposés, pour cette observable.

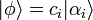
Un état peut être pur selon une observable donnée (Dans les technologies de l'information, une donnée est une description élémentaire, souvent codée, d'une chose, d'une transaction, d'un événement, etc.), et être superposé selon une autre observable. C'est d'ailleurs la raison fondamentale (En musique, le mot fondamentale peut renvoyer à plusieurs sens.) du principe d'incertitude d'Heisenberg : un état quantique qui est pur pour une observable (et qui possède donc une valeur précise pour cette observable), peut avoir tout (Le tout compris comme ensemble de ce qui existe est souvent interprété comme le monde ou l'univers.) un ensemble de valeurs possibles pour une autre observable.

Après l'opération de mesure, le système physique (La physique (du grec φυσις, la nature) est étymologiquement la « science de la nature ». Dans un sens général et ancien, la physique...) mesuré sera dans l'un des états propres définis par l'observable (postulat d'effondrement de la fonction d'onde)

Exemples d'observables

• l'hamiltonien (associé à l'énergie (Dans le sens commun l'énergie désigne tout ce qui permet d'effectuer un travail, fabriquer de la chaleur, de la lumière, de produire un mouvement.) du système)
• l'impulsion
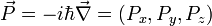
• la position .
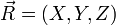
• la vitesse (On distingue :)
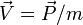
• le moment cinétique orbital (Le moment cinétique orbital est un concept de la mécanique quantique. C'est un cas particulier de moment cinétique quantique.)
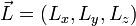
• le spin (Le spin est une propriété quantique intrinsèque associée à chaque particule, qui est caractéristique de la nature de la...)
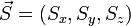
• le moment magnétique (En magnétostatique, soit une distribution de courants permanents à support compact de volume V.)

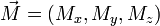
Propriétés de l'opérateur Observable

Cet opérateur doit posséder les propriétés suivantes pour pouvoir être qualifié d'observable :

• doit être un opérateur linéaire.
• Les valeurs propres de , autrement dit les résultats possibles de l'opération de mesure, doivent être des nombres réels. Ceci est assuré si est un opérateur hermitien (Plusieurs entités mathématiques sont qualifiées d'hermitiennes en référence au mathématicien Charles Hermite.).
• Les vecteurs propres de doivent être orthogonaux. Ceci est fondamental pour une observable car une fois qu'un état quantique possède une valeur définie, celle-ci doit rester la même si on applique de nouveau le même opérateur de mesure. La probabilité de trouver, comme résultat d'une seconde ( Seconde est le féminin de l'adjectif second, qui vient immédiatement après le premier ou qui s'ajoute à quelque chose de nature identique. La seconde est une unité de mesure du...) application de l'opérateur, un autre vecteur propre (En mathématiques, le concept de vecteur propre est une notion algébrique s'appliquant à une application linéaire d'un espace dans lui-même. Il correspond à l'étude des axes privilégiés, selon lesquels l'application se comporte...) doit donc être nulle. Ceci est assuré si et seulement si les vecteurs propres sont orthogonaux.
• Les vecteurs propres de doivent former une base de . Cela assure que tout état quantique (tout vecteur de ) est mesurable par cet opérateur. C'est cette base qui caractérise l'observable. Passer (Le genre Passer a été créé par le zoologiste français Mathurin Jacques Brisson (1723-1806) en 1760.) d'une observable à une autre (par exemple de la position à l'impulsion) équivaut à examiner le vecteur représentant l'état quantique dans une base ou dans une autre.
• Les vecteurs propres de doivent être normalisables. En effet, si un vecteur propre n'est pas normalisable, la probabilité d'obtenir cet état propre comme résultat d'une mesure sera nulle. Cette dernière propriété n'est pas strictement indispensable pour que soit une observable théorique, mais elle l'est pour que soit une observable correspondant à une opération de mesure réelle. Par exemple, la position ou l'impulsion ne sont pas des observables normalisables (ce qui est logique (La logique (du grec logikê, dérivé de logos (λόγος), terme inventé par Xénocrate signifiant à la fois raison, langage, et raisonnement) est dans une...), car étant des variables continues, la probabilité d'obtenir une position ou une quantité de mouvement (En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et la masse d'un objet. La quantité de mouvement d'un système fait partie,...) précise est effectivement nulle).