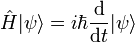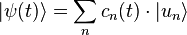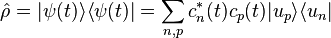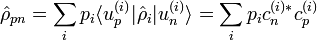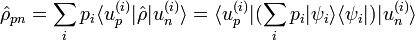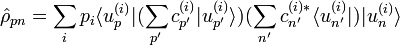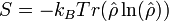Matrice densité - Définition

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique · Superposition · Observable · Intrication · Mesure · Principe d'incertitude · de correspondance · Dualité · Décohérence Expériences Fentes de Young · Expérience de Stern et Gerlach · Chat de Schrödinger · Gomme quantique · Paradoxe EPR · Téléportation quantique · Expérience d'Aspect Formalisme Notation Bra-Ket · Équation de Schrödinger · Matrice densité · Représentation de Schrödinger · de Heisenberg · d'interaction Statistiques Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion · Bose-Einstein · Boson Théories avancées Théorie quantique des champs · Axiomes de Wightman · Électrodynamique quantique · Chromodynamique quantique · Gravité quantique · Diagramme de Feynman Interprétations Problème de la mesure · Copenhague · Ensemble · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique quantique · Réduction par l'observation (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

La matrice densité, ou opérateur densité est une entité mathématique introduite par le mathématicien et physicien John von Neumann. Elle permet de résumer en une seule matrice tout l'ensemble possible des états quantiques d'un système physique donné à un instant donné, mariant ainsi mécanique quantique et physique statistique.

Définition

Cas pur

La description du système se fait ici grâce à un vecteur d'état que l'on peut développer sur la base des  :

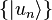
avec

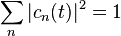
L'opérateur densité est défini pour un état pur par :

Mélange statistique d'états purs

En admettant qu'un certain système physique puisse être, à un certain instant t, dans un mélange statistique (fini ou infini) d'états quantiques avec des probabilités p_i (où ) , alors la matrice densité représentant l'ensemble de ces états est :

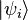
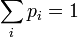
L'aspect statistique introduit ici est de deux natures, l'une classique et l'autre quantique :

1. classique : dû à l'estimation du ket par une distribution statistique des différents kets possibles,

2. quantique : incertitude quantique fondamentale même si le système est parfaitement déterminé.

Les éléments de la matrice densité valent :

où

d'où

 

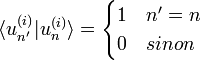
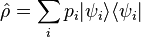
Lien avec l'entropie

Enfin, on peut définir l'entropie de Von Neumann :

où k_B est la constante de Boltzmann.

L'entropie d'un état pur est nulle, car il n'y a aucune incertitude sur l'état du système. On peut aussi trouver une base où la matrice est diagonale, avec des 0, et un 1 sur la diagonale, ce qui donne bien une entropie égale à 0.