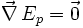Mécanique statique - Définition

Condition sur l'énergie potentielle

Dans le cas où le système est soumis à un ensemble de forces conservatives, une position d'équilibre est obtenue quand l'énergie potentielle est stationnaire, c'est-à-dire quand :

Lorsque l'énergie potentielle est à un niveau minimal local strict et que le système a un nombre fini de degrés de liberté, le théorème de Lejeune-Dirichlet montre que l'équilibre est stable, ce qui signifie que si on écarte très peu le système de ce point d'équilibre (position et vitesse), le système ne s'écartera que très peu de sa position d'équilibre (sa position restera proche de la position d'équilibre et sa vitesse restera petite). Le pendule pesant est au repos dans une position d'équilibre stable (énergie potentielle minimale) quand il se situe à la verticale de son point d'articulation.

Dans tous les autres cas, (lorsque l'énergie potentielle n'atteint par un minimum strict), l'équilibre est instable. Exemples :

• Si on retourne le pendule (rigide) pesant au-dessus de son axe, on peut espérer le placer dans une situation d'équilibre évidemment précaire. Ce sont ces cas plus spectaculaires que recherchent les équilibristes.
• Si on place une bille au fond d'une cuvette dont le fond est plat et horizontal (cas d'un minimum non strict de l'énergie potentielle), un petit coup donné à la bille écarte "beaucoup" cette bille.
• Cas d'une valeur stationnaire de l'énergie potentielle: un grimpeur debout sur une corniche au-dessus du vide.

Frontière d'isolement

Le système considéré est en équilibre sous l'effet d'actions extérieures. Cette notion est donc tributaire d'une frontière qu'il convient de bien définir, et qui constitue une surface fermée autour du système. À travers cette frontière les actions émanant d'éléments matériels situés à l'extérieur sont de deux natures:

• les actions de contact, dans ce cas le point d'application est un élément de la frontière. C'est le cas commun des liaisons mécaniques.
• les actions à distance appliquées sur une partie ou l'ensemble des points à l'intérieur de la frontière. C'est le cas des forces d'attraction ou forces électromagnétiques.

Si cette frontière est évidente quand on étudie un point matériel ou un solide, sa définition est plus subtile lorsqu'on s'intéresse à un élément de milieu continu ou une partie seulement d'un solide. À la frontière virtuelle de ces systèmes apparaissent alors des actions mécaniques bien réelles qui requiert souvent des modélisations plus complexes que celle du vecteur force.