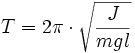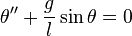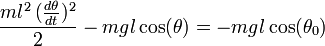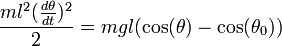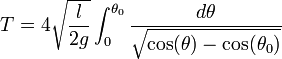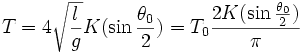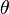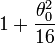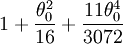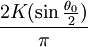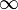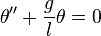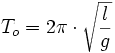Pendule pesant - Définition

Introduction

On appelle pendule pesant tout solide mobile autour d'un axe (en principe horizontal) ne passant pas par son centre de gravité et placé dans un champ de pesanteur. Déplacé de sa position d'équilibre (stable) dans laquelle le centre de gravité est à la verticale de l'axe, le solide se met à osciller de part et d'autre de cette position dite d'équilibre. Un balancier d'horloge, une balançoire, etc, constituent des pendules pesants.

Le cas le plus simple est le pendule constitué d'un petit objet pesant accroché à un fil (ou une tige) de masse négligeable devant celle de l'objet. Un tel pendule est appelé pendule pesant simple.

Le pendule pesant simple a une importance historique du fait que Galilée l'a étudié de façon détaillée et scientifique.

Étude théorique du modèle du pendule pesant simple

On peut établir l'équation différentielle du mouvement d'oscillation simplement à partir de la conservation de l'énergie mécanique. En négligeant les frottements, l'énergie mécanique du pendule est constante : elle est la somme de l'énergie cinétique et de l'énergie potentielle.

Dans le cas du modèle du pendule pesant simple, on considère que l'objet se ramène à une masse ponctuelle m, qui se déplace à la distance l de l'axe (longueur du fil ou de la tige, considérée inextensible et sans masse). On en déduit :

avec

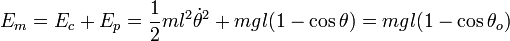
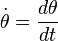
• g est l'accélération de la pesanteur.
• θ est l'angle que fait le pendule, à une date t, avec la verticale
• θ₀ est l'angle maximal.

L'énergie mécanique étant constante dans le temps, sa dérivée est nulle. En dérivant la relation ci-dessus par rapport au temps on obtient après simplification :

Cette équation est celle d'un oscillateur non harmonique, c’est-à-dire non sinusoïdal.

La période T des oscillations dépend de l'amplitude du mouvement.

Par contre, la période ne dépend pas de la masse.

Expression exacte de la période des oscillations

En séparant les variables dans  :

et en prenant la racine de cette dernière expression

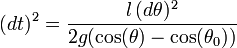
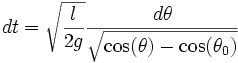
on obtient l'expression exacte de la période d'oscillations d'amplitude θ₀ qui est :

Cette expression se déduit facilement en constatant que T= 4 fois le temps mis pour aller de 0 à θ_o

où K est une intégrale elliptique complète de première espèce qui vaut en première approximation et où .

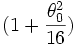
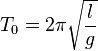
L'expression est connue sous le nom de formule de Borda.

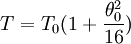
On peut également exprimer T sous forme de série. Si on pose , alors :

, où est un coefficient binomial.

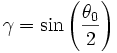
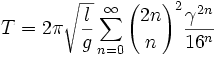
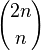
Si on développe γ en fonction de θ₀, on obtient :

.

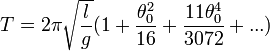
le tableau ci dessous donne les angles en degré, puis en radian dans les deux premières colonnes

ainsi que les valeurs de , , et enfin  :

Évaluation de la qualité des approximations faites

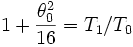
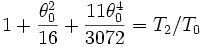
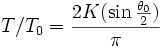
10	0,175	1,00	1,00	1,00
20	0,349	1,01	1,01	1,01
30	0,524	1,02	1,02	1,02
40	0,698	1,03	1,03	1,03
50	0,873	1,05	1,05	1,05
60	1,047	1,07	1,07	1,07
70	1,222	1,09	1,10	1,10
80	1,396	1,12	1,14	1,14
90	1,571	1,15	1,18	1,18
100	1,745	1,19	1,22	1,23
110	1,920	1,23	1,28	1,30
120	2,094	1,27	1,34	1,37
130	2,269	1,32	1,42	1,47
140	2,443	1,37	1,50	1,60
150	2,618	1,43	1,60	1,76
160	2,793	1,49	1,71	2,01
170	2,967	1,55	1,83	2,44
180	3,142	1,62	1,96

On peut retenir qu'à un angle de θ_o de 50° la période est 5% plus grande que celle donnée par la formule simple : et que la correction due au second terme n'est perceptible qu'à des angles supérieurs à 70°

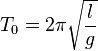
Expression approchée de la période de petites oscillations

Pour de faibles oscillations, l'équation différentielle peut approximativement s'écrire :

On voit donc que, pour de faibles amplitudes permettant d'approcher le sinus à son angle, le pendule se comporte comme un oscillateur harmonique. La période est alors indépendante de l'amplitude. On appelle ceci l'isochronisme des petites oscillations. Cette période s'exprime alors simplement par :

conformément à la limite de l'expression de Borda.

Période du pendule pesant composé

Pour un pendule pesant quelconque, l'effet de l'inertie sur la rotation ne peut pas être ramenée à une masse ponctuelle placée au centre de gravité. C'est l'ensemble du solide qui tourne, et son inertie est caractérisée par son moment d'inertie noté J et la distance l du centre de gravité à l'axe.

Aux faibles amplitudes, l'isochronisme des oscillations est aussi vérifié et la période correspondante s'exprime en fonction de J par :

; (pour le pendule simple J= m.l²)