Mesure physique - Définition

Citations

« In physical science a first essential step in the direction of learning any subject is to find principles of numerical reckoning and practicable methods for measuring some quality connected with it. I often say that when you can measure what you are speaking about and express it in numbers you know something about it; but when you cannot measure it, when you cannot express it in numbers, your knowledge is of a meager and unsatisfactory kind: it may be the beginning of knowledge, but you have scarcely, in you thoughts, advanced to the stage of science, whatever the matter may be. »

— William Thomas Thomson, Lord Kelvin, Electrical Units of Measurement (1883), Popular Lectures and Addresses (1891), Vol. I, 80-I

« En sciences physiques, une première étape essentielle dans l'apprentissage d'un sujet est de trouver comment l'appréhender en chiffres, et des méthodes pour mesurer une qualité qui lui est liée. Je dis souvent que si vous pouvez mesurer ce dont vous parlez et l'exprimer en chiffres, vous en savez quelque chose; mais si vous ne pouvez le mesurer, le quantifier, votre connaissance est d'une bien pauvre et insatisfaisante espèce: ce peut être le début de la connaissance, mais vous n'avez pas encore, dans vos pensées, avancé jusqu'au stade de science, quel que soit le sujet. »

— Traduction

Difficultés de mesure et calcul de l'incertitude

Difficultés de mesure

Pour certaines quantités physiques, l'obtention de mesures précises peut être (très) difficile. L'exactitude absolue ne peut être atteinte : des mesures répétées vont varier en raison de différents facteurs comme la température, le temps, les champs électromagnétiques, et, évidemment, de la méthode de mesure. Ainsi la vitesse du son conserve tout de même une variance puisque sa valeur varie selon les conditions dans lesquelles la mesure est faite. Des techniques statistiques sont appliquées sur des échantillons de mesure afin d'estimer cette vitesse. Dans les campagnes plus anciennes de mesures, la variance était plus importante, et comparer les résultats indiquait que la variance et le biais n'étaient pas pris correctement en compte. Une preuve de ce fait a été fournie lorsque pour des groupes de mesures variés ont été tracés avec la vitesse estimée et les barres d'erreurs, indiquant la variance attendue de la vitesse estimée d'après la valeur actuelle, les barres d'erreurs de chaque expérience ne se superposent pas toutes. Ceci indique que certains groupes ont considéré de manière incorrecte les sources d'erreurs potentielles et surestimé la précision de leurs méthodes.

Calcul d'incertitude

L'une des caractéristiques principales de la mesure physique est l'incertitude qu'elle possède intrinsèquement. Si elle est manifeste au niveau nanoscopique (grandeurs "quantiques") ou inférieures, en vertu du principe d'incertitude énoncé par Werner Heisenberg (concernant le couplage entre impulsion et position), elle existe à toute échelle. De manière générale, et si l'on considère la grandeur mesurée comme exactement différentiable, l'incertitude sur la mesure peut être exprimée selon cette différentielle :

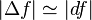
Un exemple : mesure sur un gaz parfait

Prenons l'exemple d'un gaz considéré comme parfait et obéissant donc à la loi : PV = nRT où P désigne la pression, V le volume occupé, n la quantité de matière, R est la constante des gaz parfaits et T la température du système. Pour cet exemple, la grandeur mesurée choisie est la pression P (au moyen d'un manomètre) telle que :

.

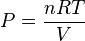
L'incertitude de mesure (ΔP) est donc :

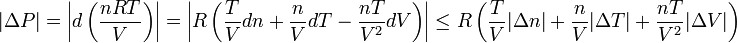
L'incertitude sur la pression est donc fonction du triplet (n,V,T) et des erreurs de mesures de ces trois grandeurs.