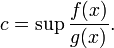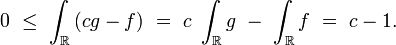Méthode de rejet - Définition
La liste des auteurs de cet article est disponible ici.
But
La méthode de rejet est utilisée pour engendrer indirectement une variable aléatoire

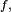
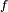
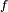
Soit
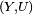
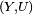


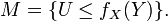
Autrement dit,
Pour simuler une suite de variables aléatoires réelles
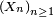
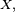
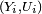
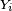
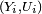
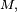
Généralisations
Le fait que
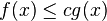
-
-
- Tant que U / h(X) > 1, reprendre en 1;
-
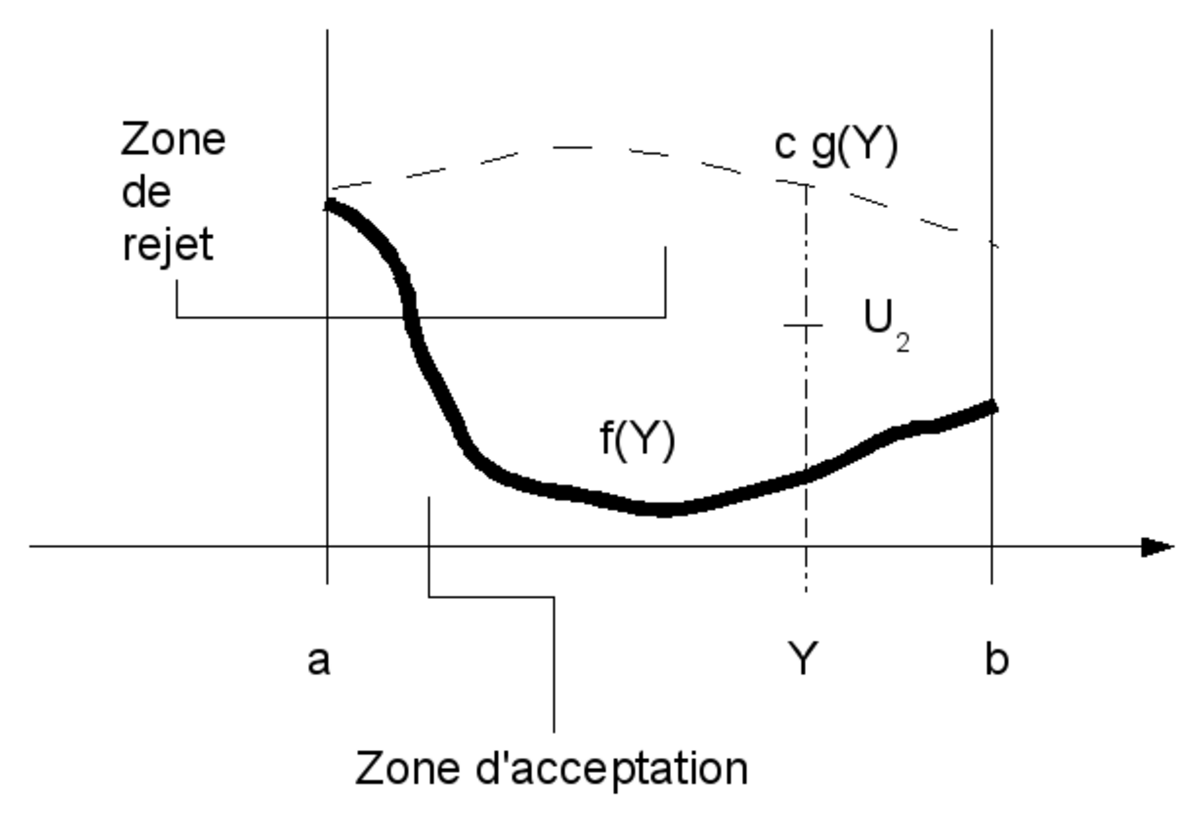
Une autre généralisation peut être considérée lorsque l'évaluation du ratio f/g est délicate. On cherche alors à encadrer la fonction f par deux fonctions facilement évaluables:
tout en supposant qu'il existe une densité g telle que
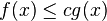
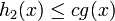
- Suite := vrai
- Tant que Suite
- tirer Y selon g;
- tirer U selon la loi uniforme U(0;1), indépendamment de Y;
- Z := U c g(Y);
- Suite := SI(
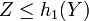
- Si Suite alors
- Si
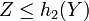
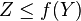
- Si
- Fin si
- fin tant que
- retourne Y comme un tirage de f.
Dans cet algorithme, les fonctions h permettent de recourir à une comparaison à f (et donc son évaluation) que très rarement.
Algorithme
On voudrait simuler une variable aléatoire réelle

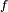
- qu'il existe une autre densité de probabilité

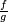

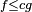
- qu'on sache simuler
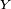
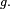
La version basique de la méthode de rejet prend la forme suivante:
- Boucler:
- Tirer
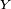
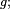
- Tirer
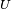
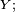
- Tirer
- Tant que
 reprendre en 1;
reprendre en 1; - Accepter
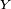
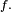
On remarque que l'algorithme comporte une boucle dont la condition porte sur des variables aléatoires. Le nombre d'itérations, notons-le
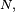
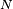
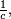
En effet,
est la probabilité, lors d'une itération, de terminer la boucle, et, par conséquent, d'accepter Y. Par suite, l'espérance de
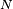
On a donc tout intérêt à choisir c le plus petit possible. En pratique, une fois la fonction g choisie, le meilleur choix de c est donc la plus petite constante qui majore le ratio f/g, c'est-à-dire:
Notons que, soit c est supérieur strict à 1, soit f=g, la deuxième alternative étant assez théorique : en effet, comme
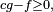
On a donc intérêt à choisir c le plus proche de 1 possible, pour que le nombre d'itérations moyen soit proche de 1 lui aussi. Bref, le choix de l'enveloppe g est primordial:
- le tirage de la loi g doit être facile ;
- l'évaluation de f(x)/g(x) doit être aisée ;
- la constante c doit être la plus petite possible ;
- la fonction cg doit majorer la densité f.
Les deux derniers points conduisent à rechercher une fonction g dont le graphe "épouse" étroitement celui de f.
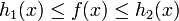
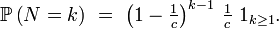
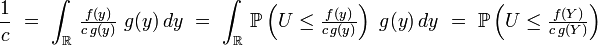
![\mathbb{E}\left[N\right]\ =\ c.](https://static.techno-science.net/illustration/Definitions/autres/1/1c378074b3893ea8e91ae6ec12edf96a_e33f254d9ae421382f0f86be4abc1c5c.png)