Nombre de Carmichael - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En théorie des nombres, un nombre de Carmichael est un entier composé positif n qui vérifie la propriété
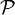
- pour tout entier a, n est un diviseur de an − a
Tour d'horizon
Le petit théorème de Fermat énonce que les nombres premiers ont la propriété
Plus les nombres deviennent grands et plus les nombres de Carmichael deviennent rares, la majorité d'entre eux rendent le test de primalité de Fermat largement inutile comparé aux autres tests de primalité comme le test de primalité de Solovay-Strassen. Par exemple, le 646e nombre de Carmichael vaut 993 905 641 et il existe 105 212 nombres de Carmichael entre 1 et 1015.
Une caractérisation des nombres de Carmichael est donnée par le théorème de Korselt en 1899.
Théorème (Korselt 1899) : Un entier positif composé n est un nombre de Carmichael si et seulement si aucun carré de nombre premier ne divise n (on dit que n est quadratfrei (sans carré)) et pour chaque diviseur premier p de n, le nombre p − 1 divise n − 1.
Il découle de ce théorème que tous les nombres de Carmichael sont des produits d'au moins trois nombres premiers impairs différents.
Korselt fut le premier à observer ces propriétés, mais il n'a pas pu trouver d'exemples de nombre de Carmichael. En 1910, Robert Daniel Carmichael trouva le plus petit de ces nombres, 561, et ceux-ci furent nommés en son honneur.
Ce nombre de Carmichael 561 peut être vérifié avec le théorème de Korselt. Effectivement, 561 = 3 · 11 · 17 n'est pas divisible par un carré de nombre premier, et 3 - 1 = 2, 11 - 1 = 10 et 17 - 1 = 16 sont tous trois des diviseurs de 560.
Les premiers nombres de Carmichael sont :
- 561 = 3 · 11 · 17
- 1 105 = 5 · 13 · 17
- 1 729 = 7 · 13 · 19
- 2 465 = 5 · 17 · 29
- 2 821 = 7 · 13 · 31
- 6 601 = 7 · 23 · 41
- 8 911 = 7 · 19 · 67
La suite des 33 premiers nombres de Carmichael en ordre croissant est donnée par la suite n°A002997 de l'Encyclopédie électronique des suites entières (OEIS), et la suite des 8241 premiers nombres de Carmichael (classés par ordre croissant et décomposés en leurs facteurs premiers) est donnée ici.
J. Chernick démontra un théorème en 1939 qui peut être utilisé pour construire un sous-ensemble de nombres de Carmichael. Le nombre (6k + 1)(12k + 1)(18k + 1) est un nombre de Carmichael si ses trois facteurs sont tous premiers. On ne sait pas si cette formule, ou d'autres similaires, engendre une infinité de nombres de Carmichael lorsque k décrit l'ensemble des entiers.
Paul Erdős soutint de manière heuristique qu'il devrait y exister une infinité de nombres de Carmichael. Cette conjecture a été démontrée en 1994 par William Alford, Andrew Granville et Carl Pomerance, et même, plus précisément, pour un n suffisamment grand, il existe au moins n2/7 nombres de Carmichael compris entre 1 et n.
Richard G. E. Pinch démontra quant à lui que pour tout n, il n'y a pas plus de
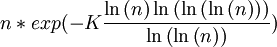
Le tableau suivant donne les valeurs approximatives de cette constante:
| n | K |
| 4 | 2,19547 |
| 6 | 1,97946 |
| 8 | 1,90495 |
| 10 | 1,86870 |
| 12 | 1,86377 |
| 14 | 1,86293 |
| 16 | 1,86406 |
| 18 | 1,86522 |
| 20 | 1,86598 |
Tel qu'en décembre 2007, il a été montré qu'il existe 8220777 nombres de Carmichael jusqu'à 1020
Propriétés
Les nombres de Carmichael ont au moins trois facteurs premiers.
Les premiers nombres de Carmichael avec respectivement au moins k = 3, 4, 5,... facteurs premiers sont (suite A006931 de l'OEIS) :
| k | |
|---|---|
| 3 | 561 = 3 · 11 · 17 |
| 4 | 41041 = 7 · 11 · 13 · 41 |
| 5 | 825265 = 5 · 7 · 17 · 19 · 73 |
| 6 | 321197185 = 5 · 19 · 23 · 29 · 37 · 137 |
| 7 | 5394826801 = 7 · 13 · 17 · 23 · 31 · 67 · 73 |
| 8 | 232250619601 = 7 · 11 · 13 · 17 · 31 · 37 · 73 · 163 |
| 9 | 9746347772161 = 7 · 11 · 13 · 17 · 19 · 31 · 37 · 41 · 641 |
Les premiers nombres de Carmichael avec quatre facteurs premiers sont (suite A074379 de l'OEIS) :
| i | |
|---|---|
| 1 | 41041 = 7 · 11 · 13 · 41 |
| 2 | 62745 = 3 · 5 · 47 · 89 |
| 3 | 63973 = 7 · 13 · 19 · 37 |
| 4 | 75361 = 11 · 13 · 17 · 31 |
| 5 | 101101 = 7 · 11 · 13 · 101 |
| 6 | 126217 = 7 · 13 · 19 · 73 |
| 7 | 172081 = 7 · 13 · 31 · 61 |
| 8 | 188461 = 7 · 13 · 19 · 109 |
| 9 | 278545 = 5 · 17 · 29 · 113 |
| 10 | 340561 = 13 · 17 · 23 · 67 |
Une coïncidence amusante est la suivante : le troisième nombre de Carmichael et premier nombre de Chernick , 1729, n'est autre que le nombre de Hardy-Ramanujan, c'est-à-dire le plus petit entier positif qui peut être écrit de deux façons différentes comme la somme de deux cubes (1729 = 7 * 13* 19 = 103 + 93 = 123 + 13). Dans la même veine, le deuxième nombre de Carmichael, 1105, peut être écrit comme somme de deux carrés de plus de façons que n'importe quel entier qui lui est inférieur. Pour clôturer la séquence, le premier nombre de Carmichael 561 peut (comme n'importe quel entier naturel) s'écrire comme somme de puissances unaires d'entiers positifs de plus de façons que n'importe quel entier positif plus petit.
Démonstration du théorème de Korselt
Soit p un nombre premier qui divise un nombre de Carmichael n. On a (p+1)n=1+np+Cn2p2+...≡1 (mod p2). D'autre part (p+1)n≡pn+1 ≡ p+ 1(mod n) (La deuxième congruence découle du fait que n est un nombre de Carmichael). Si p2 divisait n, on aurait 1≡(p+1)n≡p+1 (mod p2) ce qui est impossible. Cela montre que le carré de p ne divise pas n.
n étant un nombre de Carmichael, et p un facteur premier de n, soit a une racine primitive de p (a fortiori a premier avec p).
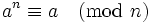
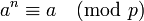
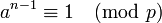
Réciproquement, supposons que n soit un produit de nombres premiers tous distincts, p1, p2, ... pk et que les nombres p1-1, p2-1, ... divisent tous n-1. Alors pour tout entier a et tout pi on a n≡1 (mod pi-1) et donc a≡api ≡a2pi-1 ≡a3pi-2≡...≡an (mod pi). Le nombre an est congru à a modulo chacun des pi, donc aussi modulo leur produit n. C'est vrai pour tout entier a, donc n est un nombre de Carmichael.
Ceci achève la démonstration du théorème de Korselt.
Conséquences du théorème de Korselt :
Soit n un nombre de Carmichael. Il est divisible par plusieurs nombres premiers disctints, donc l'un d'eux au moins est différent de deux. Appelons p ce diviseur premier impair de n. Puisque p-1 est pair, son multiple n-1 l'est aussi. Cela montre que tout nombre de Carmichael est impair.
Si p est un facteur premier d'un nombre de Carmichael n, alors modulo p-1 on a p≡1≡n et donc 1≡(n/p)p≡(n/p)1=n/p. Autrement dit, si p est un facteur premier d'un nombre de Carmichael, alors le produit des autres facteurs premiers est congru à 1 modulo p-1.
Un nombre de Carmichael ne peut être le produit de deux nombres premiers p et q, car alors chacun des deux nombres p-1 et q-1 diviserait l'autre et ils seraient égaux.
Tout nombre de Carmichael est donc le produit d'au moins trois nombres premiers impairs distincts.

















































