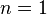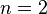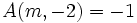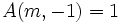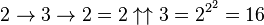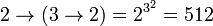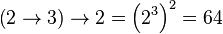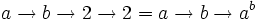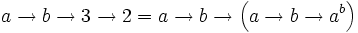Notation des flèches chaînées de Conway - Définition

Propriétés

Cette notation n'est pas associative. En effet :

La chaîne peut toujours être exprimée sous la forme , où est un nombre entier considérablement plus grand que et .

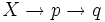
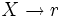
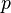
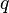
Par conséquent :

• Une chaîne commençant par est une puissance de
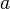
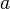
• Une chaîne commençant par 1 est égale à 1, puisqu'elle s'écrira finalement 1ⁿ=1. En fait, toute chaîne contenant un 1 peut être tronquée juste avant ce 1: pour toutes chaînes X et Y: Y peut se réduire à un nombre, et d'après la règle de réduction, se réécrit en X.
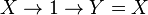
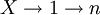
• Une chaîne commençant par est de la forme et donc égale à 4 (voir ci-dessous)/

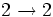
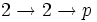
Les cas les plus simples avec quatre nombres sont :

Si pour une chaîne on définit la fonction , alors (voir Composition de fonctions).

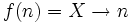
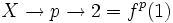
Nombre de Graham

Le nombre de Graham — qui est en 2004 le plus grand nombre jamais utilisé dans une démonstration mathématique pertinente — ne peut pas être exprimé de façon succincte dans la notation de Conway, mais si l'on définit la fonction , alors :

• et
• 

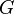
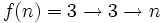
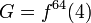
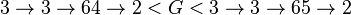
Il est possible de prouver le deuxième point :

= (3), avec 128 fois le chiffre 3

= (1)

=

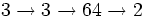
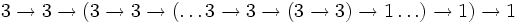
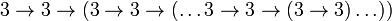
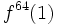
De même,

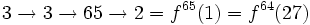
Comme est strictement croissante, , ce qui conduit à l'inégalité recherchée.

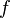
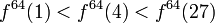
On peut noter que la simple expression est largement plus grande que le nombre de Graham.

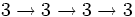
Fonction d'Ackermann

La fonction d'Ackermann peut être exprimée à l'aide de la notation de Conway :

pour

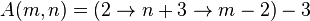
et donc :

pour

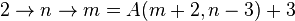
(les cas et peuvent être considérés en posant et ).