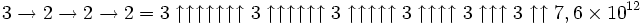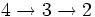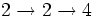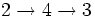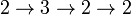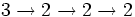Notation des flèches chaînées de Conway - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La notation des flèches chaînées de Conway est un moyen d'exprimer de très grands nombres créée par le mathématicien John Horton Conway. Elle consiste en une suite finie d'entiers positifs séparés par des flèches, comme par exemple 
.
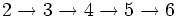
Comme beaucoup d'autres expressions combinatoires, sa définition est récursive. Au bout du compte, elle revient à élever le nombre le plus à gauche à une puissance entière et généralement énorme.
Définition
Définition des chaînes
Du point de vue de la notation, une chaîne de Conway (ou chaîne) est définie récursivement de la manière suivante:
- Tout entier positif constitue (à lui seul) une chaîne de longueur 1.
- Une chaîne de longueur n + 1 est constituée par: une chaîne de longueur n (la "queue"), suivie d'une flèche
, suivie d'un entier positif (la "tête" de la chaîne).
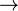
Une chaîne Y qui n'est pas incluse dans une chaîne plus longue, de la forme 
, 
, ou 
, est dite chaîne complète.
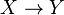
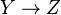
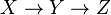
Valeur d'une chaîne
Dans la définition suivante, 
et 
sont des nombres entiers positifs et 
est une chaîne dont la valeur est supposée connue (en cela, la définition est récursive). On pose :
(exponentiation)
(et donc 
)
,
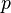
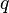
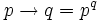
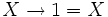
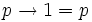
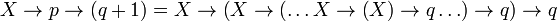
avec p copies de la chaîne X, p-1 copies de q, et p-1 paires de parenthèses.
La troisième règle (le cas général) est bien entendu le cœur de la définition. Avec ce mécanisme de réécriture, une chaîne de longueur 3 ou plus se terminant par un entier supérieur ou égal à 2 peut se réécrire sous la forme d'une chaîne de même longueur, avec un pénultième élément immensément plus grand, mais un dernier élément décrémenté d'une unité. En applicant cette règle de manière itérative, la décrémentation du dernier élément le réduit finalement à 1, ce qui permet de réduire la longueur de la chaîne d'une unité (règle 2). Après "de très nombreuses étapes intermédiaires" (pour reprendre l'expression de Knuth), la chaîne finit par être réduite à deux éléments, ce qui permet de conclure (règle 1).
Sous forme de programme récursif, la réduction s'écrit (si la chaîne est de longueur au moins deux):
function Conway(X: chaîne; p, q: Naturel): naturel begin if (X=vide) then R:=p^q elseif (q=1) then R:=Conway(Queue(X), Tête(X), p) else begin R:=Conway(X,1,1) for ctr:=1 to p-1 do R:=Conway(X,R,q-1) end return R end
NB: N'essayez surtout pas de programmer un tel programme, son temps d'exécution sera généralement supérieur à l'âge de l'univers...
Exemples simples
En explicitant un peu :
- Une chaîne de longueur 1 est juste un nombre :
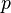
- Une chaîne de longueur 2 est un nombre élevé à une puissance entière:
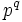
- Une chaîne de longueur 3 correspond à la notation de Knuth et à l'hyper opérateur :
.
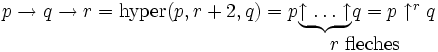
- Une chaîne de longueur 4 est généralement trop grande pour être facilement exprimée avec un opérateur de Knuth, c'est pourquoi cette notation devient pratique.
Exemples
Il est difficile de donner des exemples pertinents, car ils requièrent 4 éléments et correspondent à des nombres beaucoup trop grands pour pouvoir être explicités. Cependant, dans les exemples suivants, les numéros entre parenthèses à la fin de chaque ligne indique quelle partie de la définition de la notation a été utilisée pour passer d'une ligne à l'autre.
- =
(3) (désormais, les paires de parenthèses inutiles, comme ici, ne seront plus systématiquement indiquées) - =
(2) - =
(1) - =
(1) - =
, approximativement
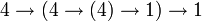
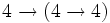
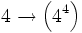
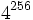
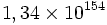
Avec la notation de Knuth : 
- =
(3) - =
(3) - =
(3) - =
(2) - =
(1) - =
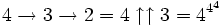
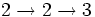
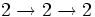
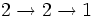
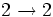
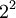
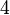
En fait, toute chaîne commençant par deux 2 est égale à 4.
- =
(3) - =
(d'après l'exemple précédent) - =
(3) - =
(2) - =
(1) - =
(1) - =
(1) - =
(3) avec 65 535 paires de parenthèses - =
(2) - =
(1) - =
(1) - =
(1) - =
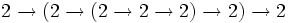
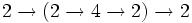
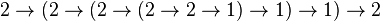
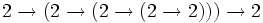
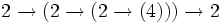
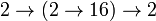
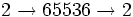
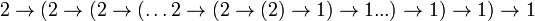
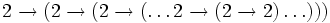
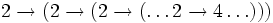
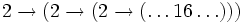
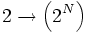
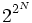
où 
est un nombre extrêmement grand.
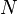
Il est possible d'écrire l'expression précédente à l'aide de la notation de Knuth :
- =
(3) - =
(1 et 2) - =
(3) - =
(voir ci-dessus) - =
(3) - =
(voir ci-dessus) - =
(id.) - =
(id.) - =
(id.) - =
(d'après l'exemple précédent)
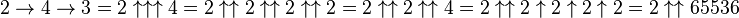
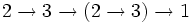
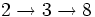
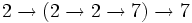
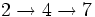
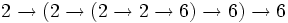
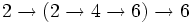
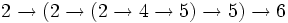
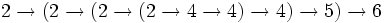
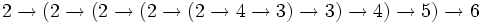
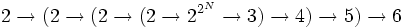
Ici, il devient impossible d'expliciter le nombre plus avant.
À l'aide de la notation de Knuth : 
.
- =
(3) - =
(1 et 2) - =
(3)
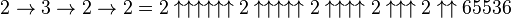
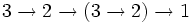
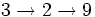
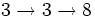
Ce qui correspond à un nombre proprement gigantesque.
À l'aide de la notation de Knuth : 