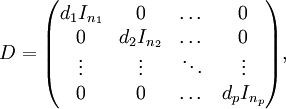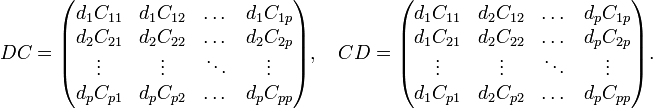Paire de matrices commutantes - Définition

L'ensemble des matrices commutant avec une matrice diagonalisable

Supposons A diagonalisable dans une extension de . Dans ce cas, on peut encore décrire l'ensemble des matrices commutant avec la matrice A.

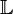
Notons I_n la matrice identité dans . Sans perte de généralité, on peut supposer que D peut se mettre sous la forme par blocs

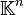
avec des tous deux à deux distincts. Dans cette matrice, seuls les blocs diagonaux peuvent être non nuls, tous les autres sont nuls. Notons C_ij le bloc de C dont les indices de lignes vont de à et dont les indices de colonne vont de à . On effectue les multiplications par blocs :

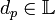
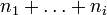
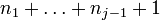
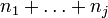
L'égalité de ces deux expressions implique que d_iC_ij = d_jC_ij pour i et j variant de 1 à p, et donc les blocs C_ij non diagonaux sont nuls.

On voit maintenant que les blocs C_jj peuvent être pris quelconques dans , et on peut conclure que C admet une forme de Jordan dans une base de vecteurs propres de D. L'ensemble des matrices commutant avec A est donc formé des matrices qui admettent une réduction de Jordan dans une base de vecteurs propres de A.

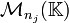
Les paires de matrices qui commutent presque sont-elles proches de paires de matrices commutantes ?

P Rosenthal a posé la question suivante en 1969 ; si le commutateur de deux matrices A et B est petit, sont elles proches d'une paire de matrices qui commutent? La question est précisée comme suit : peut-on trouver pour tout , un δ > 0 tel que pour tout entier , si A et B sont des matrices de norme inférieure ou égale à 1, vérifiant , alors il existe une paire de matrices commutantes R et S telles que .

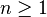
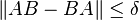
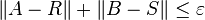
La réponse est positive si on permet à δ de dépendre de n.

La réponse négative, pour les matrices complexes, est due à Man Duen Choi, en 1988. Il énonce ainsi le théorème suivant :

Pour tout entier n > 1, il existe des matrices , A et B telles que , , et cependant , pour toute paire de matrices commutantes R et S.

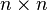
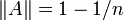
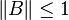
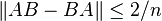
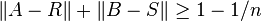
La variété commutante

Soit un corps et soit . La variété commutante est l'ensemble des couples de matrices telles que AB − BA = 0. cette variété algébrique est définie par n² équations quadratiques à 2n² inconnues. Pendant longtemps les propriétés de cette variété sont restées mystérieuses. M. Gerstenhaber a montré en 1961 que cette variété était irréductible. R. Guralnick a remarqué en 1990 que l'essentiel de cette preuve avait été donné en fait dans un article de T. S. Motzkin et O. Taussky.

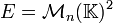
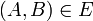
L'article de Motzkin et Taussky porte essentiellement sur les faisceaux de matrices.

Tout un pan de l'article de Gerstenhaber fait appel à des techniques de théorie des représentations, en particulier les partitions.

Il est surprenant de constater que l'étude des paires de matrices commutantes continue à être un sujet de recherche actif dans des domaines variés : algèbre commutative, algèbre numérique et computationnelle, théorie des représentations. Citons par exemple un article de Baranovsky, qui montre que la variété des paires de matrices nilpotentes est irréductible. Des travaux de 2007 et 2008 examinent la structure de Jordan des matrices commutant avec une matrice nilpotente donnée. Le sort des sous-espaces propres est encore peu abordé, mais on peut citer par exemple un travail d'Heinrich Kuhn en 1977. Sachant que les problèmes de vecteurs propres et de vecteurs propres généralisés sont toujours plus difficiles que les problèmes de valeurs propres, on voit qu'il y a du pain sur la planche.