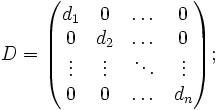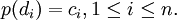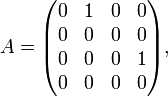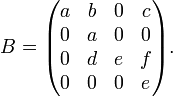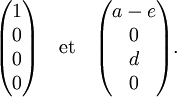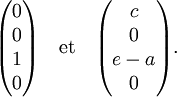Paire de matrices commutantes - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, une paire de matrices commutantes est un couple (A,B) de matrices carrées à coefficients dans un corps

L'étude des paires de matrices commutantes a des aspects tout à fait élémentaires et d'autres qui font l'objet de recherches en cours. L'énoncé de certains problèmes étudiés est assez élémentaire pour être présenté au niveau de la première année d'université. En voici un exemple :
Une matrice nilpotente est une matrice dont une puissance est nulle. On sait qu'une telle matrices est semblable à sa réduite de Jordan. Supposons la matrice A nilpotente, sous forme réduite de Jordan, avec des blocs de taille donnée. Quelle peut être la taille des blocs de Jordan des matrices nilpotentes qui commutent avec la matrice donnée A?
Bien sûr, la solution, elle, n'est pas élémentaire.
L'ensemble des matrices commutant avec une matrice dont toutes les valeurs propres sont distinctes
Le résultat le plus classique est le suivant:
Soit A une matrice

La condition sur A revient à supposer qu'il existe une matrice P inversible telle que
- P − 1AP = D;
avec
avec les di deux à deux distincts.
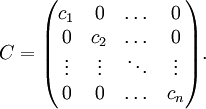
Si on suppose que AB − BA = 0, en multipliant par P − 1 à gauche et par P à droite, on obtient DC − CD = 0, avec C = P − 1BP.
On note Cij les coefficients de C. Alors, les coefficients de DC − CD valent (di − dj)Cij, ce qui implique immédiatement que les Cij sont nuls si i est différent de j. La matrice C est donc de la forme
Le théorème d'interpolation de Lagrange prouve qu'il existe un unique polynôme P de degré au plus n − 1, tel que
On a donc C = p(D). Comme Ak = (PDP − 1)k = PDkP − 1, on a également B = p(A).
Les matrices commutant avec une matrice non diagonalisable : un exemple
La situation devient très compliquée si on considère les matrices commutant avec une matrice A non diagonalisable.
Supposons d'abord que A soit une matrice de Jordan, de plus nilpotente. Un calcul élémentaire montre que toutes les matrices qui commutent avec A sont des matrices de Toeplitz triangulaires supérieures, c'est-à-dire de la forme
Si on prend comme A une matrice diagonale par blocs, dont les blocs sont des matrices de Jordan nilpotentes, il se passe des choses assez surprenantes. Notons
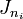
En raisonnant comme dans le paragraphe précédent, on voit que tous les blocs de la matrice B, découpés d'après la structure des blocs de la matrice A doivent vérifier la relation de commutation suivante:
- JiBij = BijJj.
Les blocs diagonaux de B sont donc triangulaires supérieurs et de Toeplitz, mais les blocs hors diagonale ne sont pas nuls ; ils sont de la forme
si
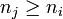
dans le cas contraire.
Rien n'indique de relation simple entre les sous-espaces caractéristiques (ou sous-espaces propres généralisés) de A et ceux de B.
Prenons le cas suivant, très simple. Soit A donné par
et choisissons la matrice B suivante :
Cette matrice commute avec A. Ses valeurs propres sont a et e, qu'on suppose distinct de a. Le sous-espace caractéristique relativement à la valeur propre a est engendré par les vecteurs
et le sous-espace caractéristique relatif à la valeur propre g est engendré par les vecteurs
Le rapport entre les sous-espaces caractéristiques de B et ceux de A n'est donc pas évident.