Paradoxe du singe savant - Définition

Démonstration

Commençons par préciser ce que l'on entend par « événements indépendants » (ici, les touches choisies successivement par le singe, qui sont censées être choisies « indépendamment » les unes des autres, c’est-à-dire que le choix de la lettre suivante ne dépend pas des lettres précédentes ; c'est le cas par exemple si le singe a une mémoire de poisson rouge). Deux événements sont dits indépendants si la probabilité pour que tous deux se produisent est égale au produit des probabilités pour que chaque événement se produise. Par exemple, si la probabilité pour qu’il pleuve sur Sydney un jour particulier est de 0,3 et la probabilité pour qu’il y ait un tremblement de terre à San Francisco un jour particulier est de 0,8, alors la probabilité pour que tous les deux se produisent le même jour est égale à 0,3 × 0,8 = 0,24.

Supposons maintenant que la machine à écrire soit pourvue de 50 touches, et que le mot à taper soit « banane ». En tapant au hasard, il y a une chance sur 50 que la première lettre tapée soit b ; de même, il y a une chance sur 50 que la deuxième lettre tapée soit a, et ainsi de suite. Ces événements sont indépendants, et ainsi il y a une chance sur 50⁶ que les six lettres du mot « banane » soient tapées. Pour la même raison, il y a à nouveau une chance sur 50⁶ que les six lettres suivantes soient celles du mot « banane », et ainsi de suite.

La probabilité de ne pas taper « banane » dans un de ces blocs consécutifs de 6 lettres est de . Comme chaque bloc est tapé indépendamment, la probabilité P_n qu'il n'y ait pas « banane » parmi les n premiers blocs de 6 lettres est .

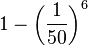
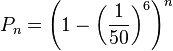
Quand n devient très grand, P_n se rapproche de 0 (c'est une suite géométrique). Pour un entier n égal à un million, P_n est égal à 0,9999, pour un n égal à 10 milliards, P_n vaut 0,53 et pour un n égal à 100 milliards, il vaut 0,0017. On dit que la probabilité P_n tend vers zéro quand n tend vers l’infini.

Ainsi, la probabilité que le singe n'ait pas tapé « banane » après 6n frappes est toujours plus petite que P_n (P_n est la probabilité que le singe n'ait pas tapé « banane » dans un des blocs consécutifs de 6 lettres ; si par exemple le singe commence en tapant « abanane », il a effectivement tapé « banane », mais il n'a pas tapé « banane » dans un des blocs qu'on a considérés). Comme P_n tend vers 0, en passant à la limite, on trouve :

La probabilité que le singe ne tape jamais « banane » vaut 0.

C'est dire que, presque sûrement, le singe tape le mot « banane » à un moment. (On peut même dire qu'il tape le mot « banane » dans un de nos blocs de 6 caractères).

L'argument précédent reste valable pour toute chaîne de caractères finie, et pour toute taille de clavier.

Pourquoi dire « presque sûrement » alors que l'événement est de probabilité égale à 1 ? Comment un événement possible peut-il être de probabilité nulle ? Il y a une subtilité due au fait que l'ensemble des résultats possibles (ici l'ensemble de toutes les chaînes de caractères infinies) est infini. Ainsi par exemple, l'événement « le singe ne tape que des "a" » fait partie des événements possibles, mais est de probabilité nulle, tout comme l'événement « le singe ne tape jamais le mot "banane" », comme on vient de le voir.