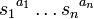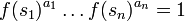Présentation d'un groupe - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Introduction informelle - Propriété universelle - Définition formelle - Le problème du mot - Exemples - Bibliographie

Introduction

En théorie des groupes, un groupe peut se définir par une présentation autrement dit la donnée d'un ensemble de générateurs et d'un ensemble de relations que ceux-ci vérifient. La possibilité d'une telle définition découle de ce que tout groupe est quotient d'un groupe libre. En général, une présentation d'un groupe G se note en écrivant entre crochets une liste de lettres et une liste minimale de mots sur cet alphabet, chaque mot étant censé valoir 1 dans le groupe et aucune relation n'existant entre les lettres, hormis celles-là et leurs conséquences. Par exemple, le groupe de présentation G=< a, b, c, d | cbcbcb, cbc^-1b^-1, b⁹ > est engendré par a, b, c, d ; dans G, le générateur b est d'ordre 9, cb est d'ordre 3, c et b commutent. Par conséquent c est d'ordre 1, 3 ou 9 et en en fait exactement 9.

Introduction informelle

Si un groupe G est engendré par un ensemble S, il est possible d'écrire tout élément de G comme un produit

x₁^a₁ x₂^a₂ ... x_n^a_n

où tous les x_i sont des éléments de S, et chaque a_i un entier relatif. Autrement dit, tout élément du groupe s'écrit comme produit des générateurs et de leurs inverses.

Si G n'est pas un groupe libre, cette écriture n'est bien sûr pas unique. Pour arriver à retrouver le groupe G, il faut préciser lesquels de ces produits sont égaux. Il suffit pour cela de spécifier quels produits sont égaux à l'élément neutre du groupe, que l'on notera 1. Il est alors intuitivement clair l'on pourra retrouver le groupe, au moins à isomorphisme près. En fait, il n'est en général pas nécessaire de préciser toutes les relations possibles, puisqu'à partir de certaines relations de bases, on peut en déduire des relations qui en sont les conséquences : par exemple, si s et t sont deux éléments de S, et si on sait que tsts=1, où 1 est l'élément neutre de G, alors on peut en déduire que (st)⁴=1, et ainsi de suite.

On arrive ainsi à la notion intuitive de définition d'un groupe par générateurs et relations, c'est-à-dire par une présentation : il s'agit de spécifier un ensemble de générateurs, le S ci-dessus, et un ensemble R de relations, qui expriment comme des produits d'éléments de S. G est alors le groupe engendré par S, et dont les générateurs vérifient seulement les relations spécifiées par R, ainsi que leurs conséquences.

Avant même de donner une définition plus précise, on peut donner quelques exemples évidents : $\mathbb Z/n\mathbb Z$ est engendré par un élément, la classe de 1. Si l'on note cet élément a, la seule relation que l'on impose est aⁿ=1.

Un autre exemple assez standard est donné par le groupe diédral D_2m, c'est-à-dire le groupe des isométries d'un polygone régulier à m côtés. Ce groupe est engendré par deux symétries orthogonales s₁ et s₂, la première par rapport à la médiatrice de l'un des segments formant les côtés du polygone, la seconde par rapport à la droite joignant le centre du polygone à l'une des deux extrémités de ce segment. Le produit des deux symétries est alors la rotation d'angle 2π/m et est donc d'ordre m. Cette relation intervient dans une présentation de D_2m (cf exemple ci-dessous).

Propriété universelle

Le groupe G=<S|R> peut être caractérisé par la propriété universelle suivante : pour tout groupe H, et pour toute application f : S→H telle que les images des éléments de S satisfassent aux relations R (i. e. telle que si ${s_1}^{a_1}\dots {s_n}^{a_n}$ appartient à R alors $f(s_1)^{a_1}\dots f(s_n)^{a_n}=1$ ), il existe un et un unique morphisme de groupe F : G→H tel que F(s)=f(s) pour tout s dans S.