Présentation d'un groupe - Définition

Définition formelle

Soient S un ensemble, F_S le groupe libre sur cet ensemble, et R une partie de ce groupe. R est l'ensemble des relations que l'on veut imposer, et pour cela, on va devoir quotienter F_S par R. Comme R n'est pas forcément un sous-groupe distingué, on va en fait quotienter par le plus petit sous-groupe distingué N contenant R.

On appelle le groupe F_S/N ainsi obtenu le groupe défini par générateurs S et relations R. On le note <S|R>. Cette écriture s'appelle une présentation du groupe. Si G est un groupe quelconque, isomorphe au groupe <S|R>, on dit que G admet <S|R> pour présentation.

Pour faire le lien avec l'introduction informelle ci-dessus, on peut remarquer que les éléments de N sont en fait les "conséquences" des relations R. On peut également remarquer que tout groupe admet une présentation : en effet, tout groupe est quotient d'un groupe libre (par exemple, le groupe libre F_G sur G). Par contre, une présentation n'est évidemment pas unique.

Un groupe est dit finiment généré s'il est généré par un ensemble S fini, et finiment présenté s'il admet une présentation de la forme <S|R>, avec S et R finis. Tout groupe finiment présenté est donc finiment généré, mais la réciproque n'est pas toujours vraie. En fait, un théorème de Bernhard Neumann (en) affirme que les groupes à deux générateurs, à isomorphisme près, forment un ensemble dénombrable, alors qu'il est facile de voir que l'ensemble des classes d'isomorphisme de groupes de présentation finie n'est pas dénombrable.

Le problème du mot

Le concept de présentation de groupe peut permettre d'effectuer simplement des calculs dans le groupe. Cependant, il faut se rendre compte qu'il a ses limites. Par exemple, il est difficile de savoir a priori si un groupe défini par générateurs et relations est trivial ou non. Le moyen le plus courant pour montrer qu'un groupe défini par présentation n'est pas trivial est de le faire agir sur un ensemble, en utilisant la propriété universelle ci-dessus. Fabriquer cet ensemble n'est pas forcément une question facile...

Plus généralement, dans un groupe de présentation G=<S|R>, il est difficile de savoir si deux mots sur S représentent ou non le même élément dans G. C'est ce qu'on appelle le problème du mot. Il a été montré que, même dans le cas des groupes de présentation finie, c'est en général un problème indécidable : il n'existe pas d'algorithme permettant de décider si deux mots sont égaux ou non.

Par contre, on peut montrer que ce problème admet une solution dans de nombreuses familles de groupes. Parmi les exemples dont certains sont décrits ci-dessus, on pourra citer les groupes abéliens de type fini, les groupes de tresses, les groupes de Coxeter, les groupes polycycliques (en), les groupes finiment présentés résiduellement finis (en). Connaître les groupes qui ont un problème du mot résoluble est un sujet de recherches actuel.

Exemples

• Le groupe libre sur S est le groupe de présentation . Par exemple, le groupe a pour présentation .

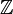
• Le groupe cyclique à n éléments a pour présentation < a | aⁿ >.

• Le groupe diédral D_2m a pour présentation .

• Le groupe symétrique est engendré par les transpositions de la forme s_i = (i,i + 1). Les relations sont alors , (s_is_{i + 1})³ = 1, et s_is_j = s_js_i pour j > i + 1. Par exemple, .

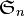
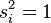
• Les deux derniers exemples sont des cas particuliers de groupes de Coxeter. Ceux-ci sont définis par une présentation, les générateurs sont des s_i et les relations qu'ils vérifient sont de la forme et , où les m_ij sont des entiers naturels.

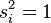
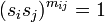
• Dans la présentation de , on peut remplacer chaque relation (s_is_{i + 1})³ = 1 par s_is_{i + 1}s_i = s_{i + 1}s_is_{i + 1}. Si de plus, on enlève les relations , on obtient une présentation du groupe de tresses B_n. Par exemple, .

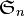
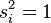
• Le groupe a pour présentation < s, t | s², t³ >.

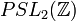
• En topologie algébrique, on obtient souvent des groupes définis par générateurs et relations, lorsque l'on veut calculer le groupe fondamental d'un CW-complexe, grâce au théorème de van Kampen. Par exemple, une présentation du groupe fondamental d'une surface de genre g est , où [a,b] désigne le commutateur aba^-1b^-1. Réciproquement, une présentation d'un groupe G permet de construire un CW-complexe de groupe fondamental G.

• Il existe aussi des groupes présentés par plusieurs générateurs et une relation. Par exemple, les groupes de Baumslag-Solitar (en) sont définis par les générateurs a,b et la relation ba^mb ^{− 1} = bⁿ.