Problème P = NP - Définition

Position des théoriciens sur cette conjecture

Les théoriciens de la complexité algorithmique pensent en majorité que P ≠ NP. C'est d'ailleurs ce relatif consensus qui justifie l'emploi de la cryptographie à clé publique pour sécuriser les transactions bancaires.

Les raisons de le penser sont en effet assez nombreuses :

• Un argument qui revient souvent est que, sans a priori, si on défend l'idée que P=NP, on peut s'attendre à ce que un algorithme polynomial résolvant un problème NP-Complet soit trouvable assez facilement, alors que si on défend P ≠ NP on s'attend à ce qu'il ne soit jamais trouvé. Le tableau de la situation, après plus de cinquante ans de recherches vaines en ce sens, est plus conforme et cohérent à P ≠ NP.

• Plus formellement, un article de Razborov et Rudich de 1993, qualifié par Scott Aaronson comme l'un des résultats les plus importants concernant le problème P=NP, tend à démontrer que la raison pour laquelle P ≠ NP est si difficile à démontrer, est que probablement P ≠ NP. Cette article montre une contradiction entre certaines conjectures très plausibles sur les générateurs de nombres pseudo-aléatoires et les procédés habituels de démonstration de P ≠ NP. Si P ≠ NP est démontrable, alors ce sera nécessairement avec des méthodes nouvelles, très différentes des méthodes habituellement employées dans les démonstrations.

• Un argument plus philosophique est de considérer qu'un monde où P=NP est très différent d'un monde où P ≠ NP. Dans un monde où P=NP, des capacités jusqu'ici réservées aux être humains (créativité, recherche..) sont potentiellement accessibles au calcul.

Statut du problème vis à vis de l'informatique quantique

Relations supposées entre la classe BQP et les autres classes de complexité.

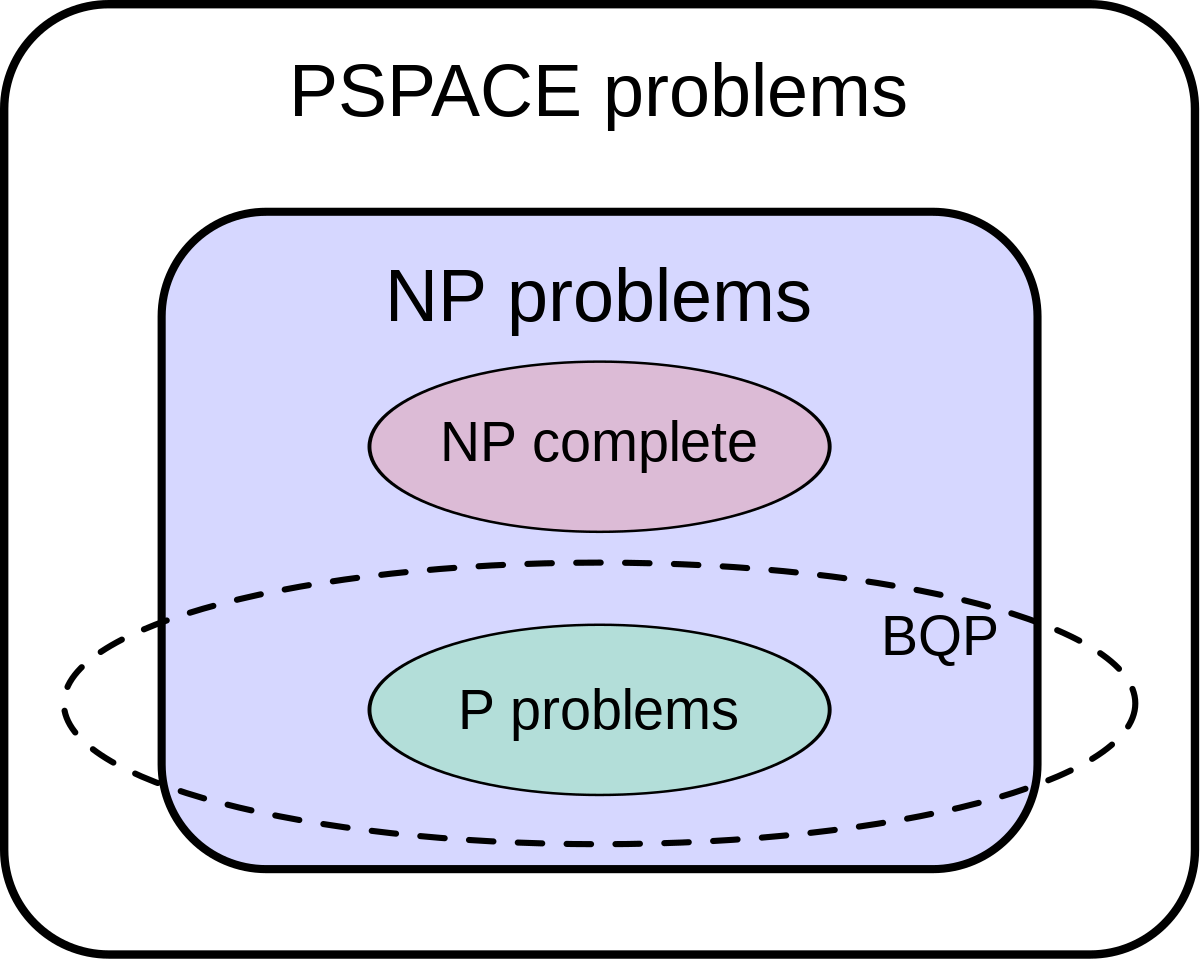
La classe des problèmes qui peuvent être résolus efficacement par des calculateurs quantiques est appellée BQP, pour "Bounded error, Quantum, Polynomial time". Les calculateurs quantiques exécutent uniquement des algorithmes probabilistes, et constitue la contrepartie de la classe de complexité BBP pour les ordinateurs classiques. La classe BQP est la classe des problèmes qui peuvent être résolus par un calculateur quantique en temps polynomial, avec une probabilité d'erreur d'au plus 1/3.

BQP est supposé disjoint de la classe NP-Complet, et un sur-ensemble de la classe P (voir schéma), mais cela n'est pas démontré. La décomposition en produit de facteurs premiers est un problème de classe NP (mais on ne sait pas s'il est NP-Complet), et BQP car il peut être résolu en temps polynomial par un algorithme quantique : l'algorithme de Shor. On pourrait donc être tenté de penser qu'un calculateur quantique serait en mesure de résoudre un problème NP-complet dans un temps polynomial.

Mais cet exemple ne donne pas d'indice édifiant en ce sens, car il se pourrait aussi que le problème de la décomposition en facteurs premier soit en fait de classe P, auquel cas l'algorithme de Shor n'apporterait rien par rapport à l'informatique classique. De plus, l'algorithme de Shor s'appuie lourdement sur la structure algébrique des nombres, ce qui n'est le cas d'aucun problème NP-Complet connu. Mais comme il n'est pas démontré que BQP est disjoint de NP-Complet, on ne peut non plus formellement écarter l'hypothèse que les problèmes NP-Complets puissent être en théorie calculable par un ordinateur quantique en temps polynomial.

Toutefois, les théoriciens s'accordent pour penser que les algorithmes quantiques ne pourront résoudre les problèmes NP-Complet en temps polynomial. Notamment, il existe un algorithme quantique qui s'applique aux problèmes NP-Complet : l'algorithme de Grover, mais qui n'est pas polynomial (bien que plus rapide que les algorithmes classiques), et il existe de forts indices selon lequels on ne pourra pas aller plus loin en matière d'algorithme quantique.

Enfin, il convient de remarquer que les calculateurs quantiques sont un type particulier de machines de Turing^{[réf. souhaitée]}. La thèse de Church s'applique donc a priori aux calculateurs quantique, qui possèdent donc les mêmes propriétés et limitations théoriques que les ordinateurs classiques. Il n'y a donc pas lieu de penser, a priori, que le problème P=NP puisse être fondamentalement différent dans le cas des calculateurs quantiques.