Quantum - Définition et Explications

Introduction

Mécanique quantique

Postulats de la mécanique quantique Histoire de la mécanique quantique Concepts fondamentaux État quantique (En mécanique quantique, l'état d'un système décrit tous les aspects du système physique. Il...) · Superposition (En mécanique quantique, le principe de superposition stipule qu'un même état quantique peut...) · Observable (Dans le formalisme de la mécanique quantique, une opération de mesure (c'est-à-dire...) · Intrication · Mesure · Principe d'incertitude · de correspondance (La correspondance est un échange de courrier généralement prolongé sur une longue période. Le...) · Dualité · Décohérence Expériences Fentes de Young (Les fentes de Young sont l'objet d'une expérience de physique réalisée en 1801 par Thomas Young...) · Expérience de Stern et Gerlach · Chat de Schrödinger (L'expérience du chat de Schrödinger fut imaginée en 1935 par le physicien Erwin...) · Gomme quantique · Paradoxe EPR (Le paradoxe EPR, abréviation de paradoxe Einstein-Podolsky-Rosen, est une expérience de...) · Téléportation quantique (La téléportation quantique est un protocole de communications quantiques consistant...) · Expérience d'Aspect Formalisme Notation Bra-Ket (La notation bra-ket a été introduite par Paul Dirac pour faciliter l’écriture...) · Équation de Schrödinger (L'équation de Schrödinger, conçue par le physicien autrichien Erwin Schrödinger en 1925, est...) · Matrice densité (La densité ou densité relative d'un corps est le rapport de sa masse volumique à la...) · Représentation de Schrödinger · de Heisenberg · d'interaction (Une interaction est un échange d'information, d'affects ou d'énergie entre deux agents au sein...) Statistiques (La statistique est à la fois une science formelle, une méthode et une technique. Elle...) Maxwell-Boltzmann · Échange · Fermi-Dirac · Fermion (Le modèle standard classe les particules élémentaires en deux grandes...) · Bose-Einstein · Boson (Les bosons représentent une classe de particules qui possèdent des propriétés...) Théories avancées Théorie quantique des champs (La théorie quantique des champs (QFT, abréviation du terme anglais Quantum field theory)...) · Axiomes de Wightman · Électrodynamique quantique (L'électrodynamique quantique relativiste est une théorie physique ayant pour but de concilier...) · Chromodynamique quantique (La chromodynamique quantique, acronyme QCD de l'anglais Quantum ChromoDynamics, est une théorie...) · Gravité quantique (La gravité quantique est une branche de la physique théorique tentant d'unifier la...) · Diagramme de Feynman (Un diagramme de Feynman est une représentation symbolique permettant de faire des calculs en...) Interprétations Problème de la mesure · Copenhague · Ensemble (En théorie des ensembles, un ensemble désigne intuitivement une collection...) · Variables cachées · Transactionnelle · Mondes multiples · Histoires consistantes · Logique (La logique (du grec logikê, dérivé de logos (λόγος),...) quantique · Réduction par l'observation (L’observation est l’action de suivi attentif des phénomènes, sans volonté de les...) (consciente) Physiciens Planck · de Broglie · Schrödinger · Heisenberg · Bohr · Pauli · Born · Dirac · von Neumann · Einstein · Bohm · Feynman · Everett · Penrose

Cette boîte : voir • disc. • mod.

En physique (La physique (du grec φυσις, la nature) est étymologiquement la...), un quantum (mot latin signifiant « combien » et qui s'écrit « quanta » au pluriel) représente la plus petite mesure indivisible, que ce soit celle de l'énergie (Dans le sens commun l'énergie désigne tout ce qui permet d'effectuer un travail, fabriquer de la...), de la quantité de mouvement (En physique, la quantité de mouvement est la grandeur physique associée à la vitesse et la masse...) ou de la masse (Le terme masse est utilisé pour désigner deux grandeurs attachées à un...). Cette notion est centrale en théorie des quanta (La théorie des quanta est le nom donné à une théorie physique qui tente de...), laquelle donnera naissance à la mécanique quantique (La mécanique quantique est la branche de la physique qui a pour but d'étudier et de...).

Description

La théorie (Le mot théorie vient du mot grec theorein, qui signifie « contempler, observer,...) des quanta ou théorie quantique, affirme que l'énergie rayonnante est discontinue. Les quanta sont alors les « grains » composants cette énergie de valeur h.ν, où :

• h est la constante de Planck (En physique, la constante de Planck, notée h, est une constante utilisée pour décrire la taille...),
• ν est la fréquence (En physique, la fréquence désigne en général la mesure du nombre de fois qu'un...) de l'onde (Une onde est la propagation d'une perturbation produisant sur son passage une variation...).

Ainsi, on peut déterminer facilement l'énergie contenue dans un photon (En physique des particules, le photon (souvent symbolisé par la lettre γ — gamma)...) en multipliant sa fréquence (déduite de sa longueur (La longueur d’un objet est la distance entre ses deux extrémités les plus...) d'onde puisque sa vitesse (On distingue :) est constante) par h.

La valeur de h est faible : 6,626.10^-34 J.s.

Et , c'est-à-dire que le quotient est toujours un multiple de h.

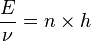
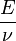
Application en Electronique

En électronique, le quantum correspond à la tension (La tension est une force d'extension.) analogique (Le concept d'analogique est utilisé par opposition à celui de numérique.) de la valeur numérique (Une information numérique (en anglais « digital ») est une information...) la plus petite dans un convertisseur numérique/analogique, soit un 1 logique. C'est donc la différence de tension qu'il y a entre une valeur numérique et la valeur numérique suivante, à la sortie d'un convertisseur numérique/analogique.

avec V_PE la Tension Pleine Echelle

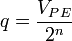
Exemple

Les suites binaires suivantes sur n=4 bits :
- De l'analogique au numérique on a :

       0 0 0 0 si Ua < 3mV 
 0 0 0 1 si 3mV  1 1 1 1 si 45mV < Ua < TPE 
 Ainsi le quantum q = 3mV ( on augmente de 3mV en analogique pour 0 0 0 1 en numérique )       
      

- Du numérique à l'analogique on a :

       0 0 0 1 = 3mV ( = q )
 0 0 1 0 = 6mV ( = 2q )
 1 1 1 1 = 45mV ( = 15q )