Problème à deux corps - Définition

Les limites de la résolution classique

Dans le cas de systèmes massifs en orbite très resserrée, l'approximation newtonienne devient insuffisante pour décrire le mouvement des deux corps, et des effets de relativité générale doivent être pris en compte. C'est notamment le cas dans les pulsars binaires. L'orbite des deux corps doit alors être décrite en faisant intervenir des paramètres supplémentaires appelés paramètres post-képleriens.

Illustrations

Quelques animations représentants les orbites de deux corps (rond blanc) autour du barycentre (croix rouge).

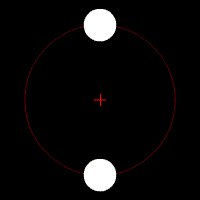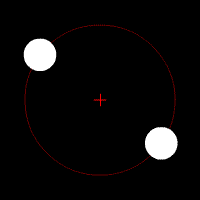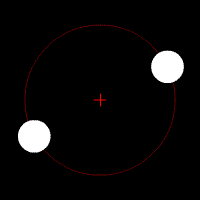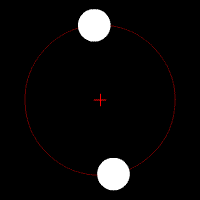Deux corps de même masse	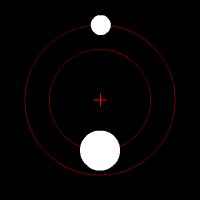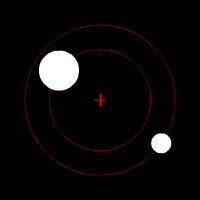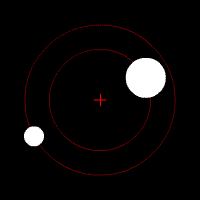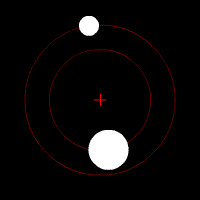Un corps de masse légèrement plus importante que l'autre	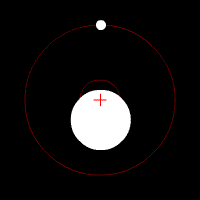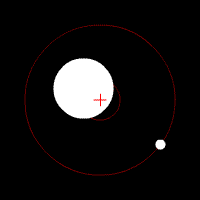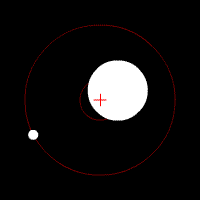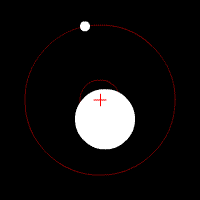Un corps de masse plus importante que l'autre	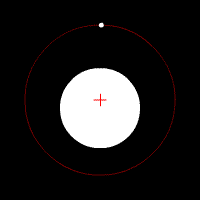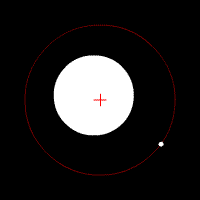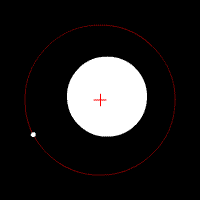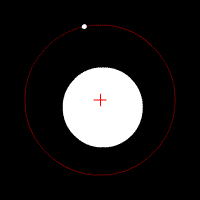Un corps de masse bien plus importante que l'autre
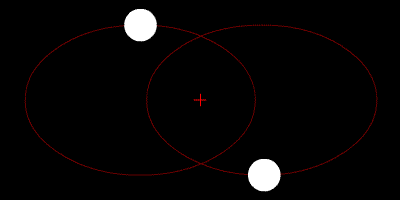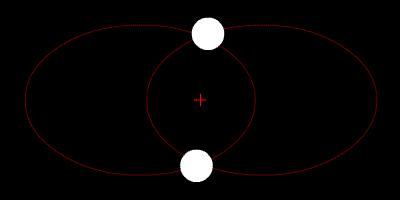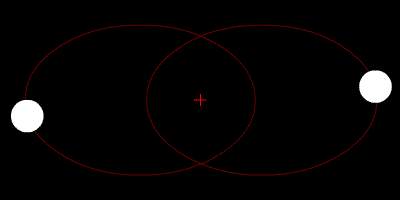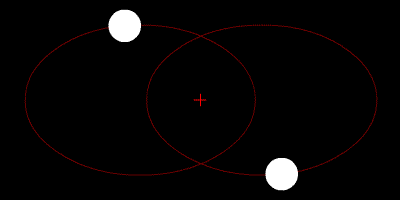Deux corps de même masse, orbites elliptiques		Un corps de masse plus importante que l'autre en mouvement linéaire